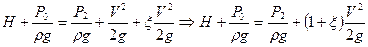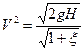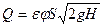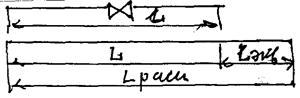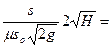Что такое эквивалентная длина
Эквивалентная длина



Иногда при расчете систем трубопроводов с большим числом местных сопротивлений потери напора вычисляют по их эквивалентным длинам. Длина прямой трубы на протяжении которой потери по длине равны потерям в данном сопротивлении является эквивалентной длиной данному сопротивлению.
Истечение жидкости через отверстия и насадки.
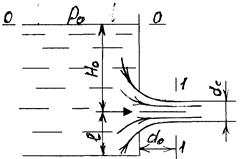
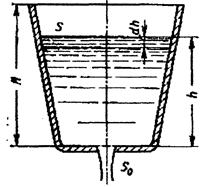
Расчет истечения жидкости через отверстия сводится к определению скорости истечения и расхода. При истечении жидкости из малого отверстия струя на расстоянии l»0,5 dотв. имеет максимальное сжатие. При расчетах сжатие струи учитывается коэффициентом сжатия e. Коэффициент сжатия струи – отношение площади Sсж сжатого сечения трубы к площади отверстия S0 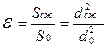
Рассмотрим истечение жидкости из малого отверстия в баке. Т.к. S1-1>>>S2-2 то скоростью в баке можно пренебречь VБ=0. Составим уравнение Бернулли: 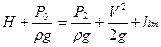
где 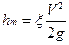
P0 – давление на поверхности.
Р2, V2 – давление и скорость жидкости в сечении 2-2.
Если Р0=Р2=Ратм то 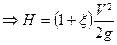
если принять 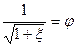
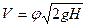
где 
Для идеальной жидкости 
Расход жидкости через малое отверстие

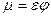
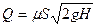
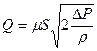
где 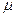
DР – расчетная разность давления под действием которой происходит истечение.
Сила давления струи жидкости на стенки.
Струя жидкости действует на твердую преграду с определенной силой, которая зависит от скорости и размеров поперечного сечения струи, формы и размеров преграды и ее расположения по отношению к струе. F=rQV(1-cosa), где
— Q – объемный расход жидкости
— V – скорость жидкости
В частном случае 
В последние десятилетия с целью увеличить стойкость инструмента, повысить качество обработки и производительность процесса резания в промышленности ведутся работы, связанные с применением не традиционных режущих инструментов и новых технологий механической обработки заготовок из различных материалов.
В настоящее время широко распространены способы обработки заготовок с использованием потока энергии от различных источников: ультразвуковая, электра эрозионная, электра химико-физическая, плазменная, лазерная, а также обработка с помощью водяной или абразивно-жидкостной струей. При двух последних способах кинетическая энергия струи жидкости, истекающей под большим давлением (Рс =100 – 1000 МПа) из отверстия малого диаметра (dс=0,05-0,5 мм), превращается в механическую энергию (работу резания). При этом скорость струи жидкости достигает (Vc=500-1000 м/с). Этот способ снижает расход материала в 15-20 раз, уменьшает силы резания (до 100 Н) благодаря чему напряжение и деформации по краям обрабатываемой детали незначительны, понижает температуру в зоне резания (60-900) и как следствие нет термодеструкции при обработке полимерных материалов и т.д. При ударе столбика воды о поверхность материала в центре удара происходит сжатие от силы воздействия струи, вызывающее появление резкого пика локального давления Рл.
Для идеально жесткой струи воды 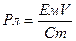
где Ем – модуль Юнга, Па;
Vc – скорость струи м/с;
См – скорость распространения волн в материале м/с.
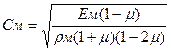
где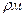
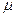
Для разрезания материала должно выполняться условие Рл³sпр. тогда
скорость определяется 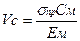
жесткой струи воды 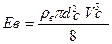
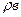
Для реализации высоких скоростей и давлений в данной установке используют мультипликатор.
2 – станция подачи и очистки технической воды.
3 – уловитель струи технической воды.
4 – головка с соплом.
5 – аккумулятор, служит для гашения пиковых давлений и стабилизации выходного давления.
Эквивалентная длина
Эквивалентной длиной называют такую длину прямого участка трубопровода данного диаметра, потери напора в котором при пропуске данного расхода равны рассматриваемым местным потерям.
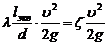
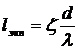
Эквивалентной длиной данного местного сопротивления называют такую длину прямого отрезка трубы, которая создает гидравлическое сопротивление, равное сопротивлению детали трубопровода, обусловившей потери напора.
Режимы движения жидкости. Основные понятия. Критерий Рейнольдса
1) Ламинарнымназывается слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При таком течении все линии тока жидкости вполне определяются формой русла. При ламинарном течении в трубе все линии тока направлены параллельно оси трубы. Ламинарное течение является упорядоченным при постоянном напоре строго установившегося течения. Ламинарный режим наблюдается преимущественно при движении вязких жидкостей (нефти, смазочных масел и т.п.), и менее вязких жидкостей при их течении с небольшими скоростями.
2) Турбулентнымназывается течение, сопровождающееся интенсивным перемешиванием жидкости и пульсацией скоростей и давления. Движение отдельных частиц оказывается хаотичным, беспорядочным. Наряду с осевым перемещением наблюдается вращательное и поперечное перемещение отдельных объемов жидкости. Этим и объясняются пульсации скоростей и давления.
— Безразмерный комплекс величин 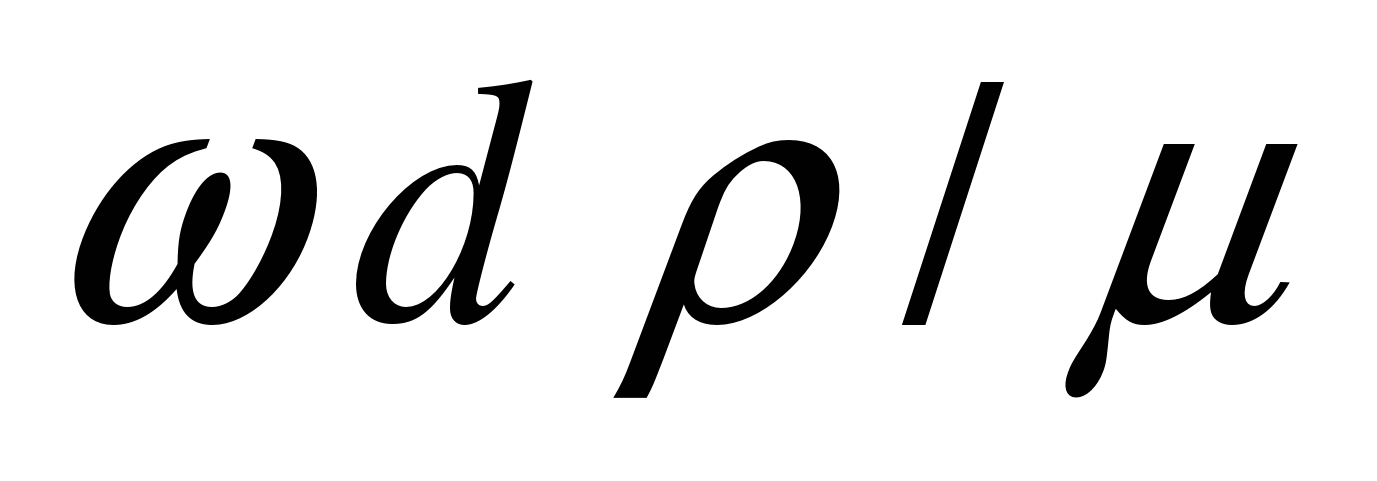
 |
При 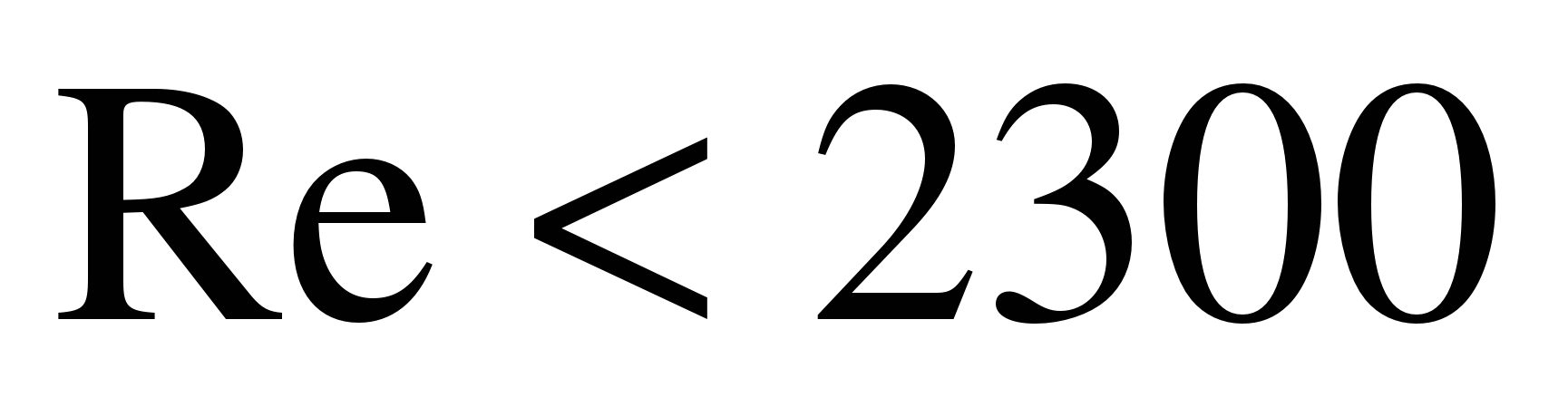
Если жидкость движется по трубе круглого сечения, то в формулу (чуть выше) подставляют внутренний диаметр трубы 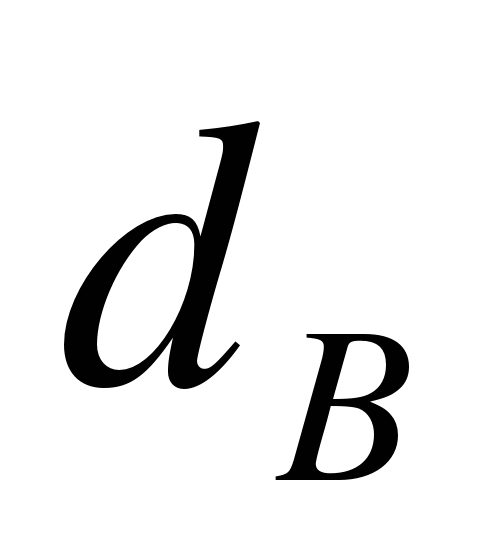
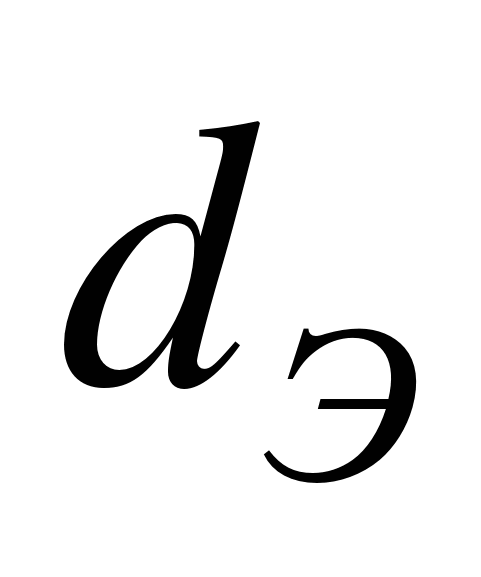
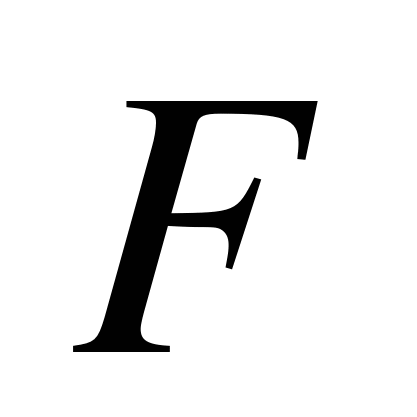
Дата добавления: 2015-04-18 ; просмотров: 12 ; Нарушение авторских прав
Местные сопротивления. Эквивалентная длина



Виды местных сопротивлений. Конструктивные элементы в трубопроводах, вызывающие местные гидравлические потери, называются местными сопротивлениями. К ним относятся задвижки (рис. 4.8, а), диафрагмы (рис. 4.8, б), колена (изгибы) (рис. 4.8, в), вентили (рис. 4.8, г), расширения, сужения (как внезапные, так и постепенные) и т.п.
Рис. 4.8. Схемы местных гидравлических сопротивлений: а — задвижка; б — диафрагма; в — колено; г — вентиль
При протекании жидкости через местные гидравлические сопротивления поток деформируется, отрывается от стенок, возникают вихри. Местные потери удельной энергии (напора) определяются формулой Вейсбаха (4.1). Если диаметр трубопровода переменный, то за расчетную скорость, подставляемую в (4.1), принимают скорость, соответствующую его меньшему диаметру.
Значения коэффициентов местных сопротивлений определяются экспериментально для конкретных видов местных сопротивлений. Для некоторых из них ζм получены теоретически.
Рассмотрим некоторые виды местных сопротивлений.
Внезапное расширение канала (трубы). Потери напора при внезапном расширении канала (рис. 4.9) по теореме Борда равны скоростному напору, определенному по разности скоростей в сечениях канала:
Согласно теореме о неразрывности струи
Из сравнения (4.23) с формулой Вейсбаха (4.1) следует:
Рис. 4.9. Внезапное расширение канала
Постепенное расширение канала — диффузор. Течение жидкости в диффузоре (рис. 4.10) сопровождается уменьшением скорости и соответственным увеличением давления, т. е. преобразованием кинетической энергии в энергию давления. У стенок уменьшение кинетической энергии жидкости может привести к тому, что слои жидкости оказываются не способными преодолеть повышение давления.
Рис. 4.10. Постепенное расширение канала — диффузор
Эти слои останавливаются или начинают двигаться в обратную сторону, что вызывает отрыв потока от стенки и вихреобразование. Отрыв и вихреобразование возрастают с увеличением угла расширения диффузора, и вместе с этим растут гидравлические потери на вихреобразование. Максимальный угол расширения диффузора αдиф, обеспечивающий безотрывность потока, составляет 8. 10°. Наиболее выгодным (оптимальным) является αдиф = 6° (рис. 4.11).
Коэффициент сопротивления можно выразить через долю потерь напора при внезапном расширении
где — коэффициент, учитывающий уменьшение потерь напора при постепенном расширении по сравнению с потерями напора при внезапном расширении с тем же соотношением сечений.
Рис. 4.11. Зависимость коэффициента сопротивления от угла расширения αдиф
Зависит от угла расширения диффузора:
Рис. 4.12. Внезапное сужение канала
Если обозначить степень сжатия струи через ε
Для практических расчетов можно пользоваться формулой И. Е. Идельчика:
где п — степень сжатия потока ( ).
Потери энергии при внезапном сужении потока рассчитываются по установившейся скорости v2 в сечении ω2 за местным сопротивлением. Коэффициент сжатия ε зависит от степени сжатия потока п и может быть определен по формуле А.Д. Альтшуля:
Для уменьшения сжатия закругляют кромку сужающего канала.
Постепенное сужение канала — конфузор. Для конфузора (рис. 4.13) коэффициент можно выразить через долю потерь напора при внезапном сужении [см. формулу (4.26)].
где — коэффициент, учитывающий уменьшение потерь напора при постепенном сужении по сравнению с потерями напора при внезапном сужении с тем же соотношением сечений. Он зависит от угла сходимости конфузора αк. Эта зависимость приведена на рис. 4.14.
| Рис. 4.13. Конфузор |
| Рис. 4.14. Зависимость коэффициента от сходимости конфузора αк |
Внезапный поворот канала. Внезапный поворот трубы или колено без закругления (рис. 4.15) вызывают значительные потери энергии в связи с отрывом потока и вихреобразованием. Эти потери тем больше, чем больше угол поворота русла 8. Потери напора рассчитывают по формуле
Зависимость коэффициента сопротивления колена от угла δ приведена на рис. 4.16. При δ = 90° ζкол = 1.
| Рис. 4.15. Колено без закругления |
Что такое эквивалентная длина


Зачастую в технической документации встречается термин «эквивалентная длинна магистрали». Под этим замысловатым названием надо понимать длину трубопровода + условную длину участков местных сопротивлений (углов, поворотов, отводов, маслоподъемных петель, запорной и регулирующей арматуры). В таблице приведены сопротивления наиболее распространенных узлов в пересчете на соответствующую их сопротивлению, эквивалентную длину.
Пример: межблочный трубопровод прецизионного кондиционера с выносным воздушным конденсатором состоит из нагнетательной (компрессор-конденсатор) и жидкостной (конденсатор-рессивер внутреннего блока) магистралей. Жидкостная магистраль диаметром 18мм (3/4″) состоит из прямых участков общей длинной 26 м., четырех колен 90°, двух колен 45°, и одного обратного клапана. Следовательно эквивалентная длинна жидкостного трубопровода составит:
Lэкв. = 26 + (4 х 0,6) + (2 х 0,3) + (1 х 2,4) = 31,4 м.
Этот расчет применяется для жидкостных магистралей. При расчете эквивалентной длинны газовых (нагнетательных) магистралей местными сопротивлениями, как правило, пренебрегают.







Отдел ВЕНТИЛЯЦИЯ. Итоги 2021 года.
По обычаю, отдел «ВЕНТИЛЯЦИЯ» компания ООО «Высокотехнологичные инженерные системы» подводит итоги в уходящем году. В первую очередь хотим выразить благодарность нашим заказчикам за плодотворное сотрудничество в 2021 году. В уходящем году, ведущий отдел нашей компании сохранил устойчивое развитие, расширив спектр деятельности по целому ряду востребованных рынком профильных направлений.
читать дальше
Контроль параметров микроклимата и качества воздуха.
23 июля 2020 года инструктивной группой компании ООО «Высокотехнологичные инженерные системы» разработаны новые методические рекомендации,
читать дальше
Определение потерь вентиляционной сети
Эквивалентная длина трубы
Иногда местные сопротивления выражают в виде эквивалентной длины прямого участка трубы. Эквивалентная длина – это длина условного трубопровода, гидравлические потери на котором равны местным потерям.
hм.с. =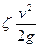
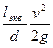
Приравниваем hм.с. = hтр, тогда 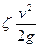
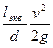
Отсюда z= l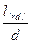
Общие потери напора h = l 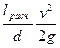
Так как коэффициент трения l зависит от числа Рейнольдса, то и эквивалентная длина трубы будет различной в зависимости от значения числа Рейнольдса.
2.6. Истечение жидкости через отверстия и насадки
Истечение жидкости через отверстия и насадки различных форм является весьма распространенным процессом. На практике часто приходится встречаться с истечением через отверстия в тонкой стенке, цилиндрические, конические сходящиеся и расходящиеся, а также коноидальные (воронкообразные) насадки. Такие элементы гидравлических систем используются в установках для разрушения и размыва породы (гидромониторы); для тушения пожаров; с целью распыления и дробления жидкости (дождевальные установки, подача топлива в камеры сгорания); для дозирования жидкости (жиклеры карбюраторов); для измерения времени опорожнения сосудов и т.д.
Этот случай движения жидкости характерен тем, что в процессе истечения часть потенциальной энергии, которой обладает жидкость в резервуаре, за исключением потерь, превращается в кинетическую энергию свободной струи.
Основными задачами является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.
2.6.1. Истечение жидкости через малое отверстие в тонкой стенке
при постоянном напоре
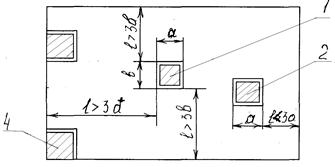
Классификация отверстий по их размерам:
где dо – диаметр отверстия; Но = const – напор в сосуде.
Кроме того, отверстия по форме могут быть круглые и некруглые.
Стенка считается «тонкой» при условии, что толщина стенки d
Пусть жидкость вытекает из резервуара в воздушное пространство с давлением р1.
При истечении жидкости через малое отверстие в тонкой стенке вследствие влияния сил инерции происходит уменьшение поперечного сечения струи по отношению к сечению отверстия. Цилиндрическую форму струя принимает на расстоянии, равном примерно одному диаметру отверстия. Здесь располагается «сжатое сечение», в котором площадь струи минимальна.
1 – совершенное сжатие, 2 – несовершенное полное сжатие, 3 и 4 – неполное сжатие.
Запишем уравнение Бернулли в напорах для сечений 0-0 и 1-1:
Н = 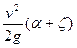
v = 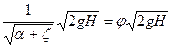
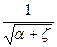
Для идеальной жидкости z = 0, a = 1, тогда j = 1 и vт = 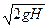
Коэффициент скорости выражает отношение действительной скорости истечения к теоретической j = vд /vт £ 1. Уменьшение действительной скорости по отношению к теоретической происходит за счет потери части напора при истечении реальной жидкости.
Если истечение происходит в атмосферу, то давление по всему сечению цилиндрической струи равно атмосферному.
Теоретический расход Qт = sovт = so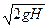
Значения коэффициентов истечения зависят прежде всего от типа отверстия или насадка, а также от числа Рейнольдса.
На рисунке показаны зависисмости коэффициентов e,j и m для круглого малого отверстия от Reи, подсчитанного по идеальной скорости истечения:
Reи = 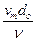
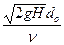
При больших значениях чисел Рейнольдса – квадратичная область истечения.
При расчетах для маловязких жидкостей обычно принимают следующие значения коэффициентов истечения:
При истечении жидкости под действием сил поверхностного натяжения происходит изменение формы струи по отношению к форме отверстия. Это явление называется инверсией струи.
2.6.2. Истечение через насадки при постоянном напоре
Коноидальный насадок, или сопло, близок по форме естественно сжимающейся струе. Он очень распространен, так как имеет очень малые потери и поэтому коэффи-циент расхода близок к единице.
Рассмотрим истечение через внешний цилиндрический насадок.
Возможны два режима истечения жидкости через цилиндрический насадок: со сжатием и без сжатия струи.
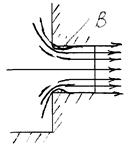
1-й режим. При входе в насадок струя слегка сжимается, а затем постепенно расширяется до размеров отверстия и выходит полным сечением.
В – область завихренности потока.
Так как коэффициент сжатия струи e = 1, тогда коэффициент скорости равен коэффициенту расхода j = m..
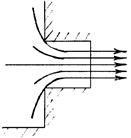
2-й режим. При некотором соотношении l/d и Re наступает 2-й режим истечения, когда струя сжимается и выходит из насадка сжатым сечением.
Напор, при котором происходит переход от одного режима к другому, называется критическим. При напоре, равном критическому, происходит внезапное изменение режима истечения. При Н > Нкр. 1-й режим истечения невозможен.
Таблица коэффициентов истечения отверстий и насадков
в квадратичной области истечения
2.6.3. Истечение при переменном напоре
Рассмотрим истечение жидкости в атмосферу при переменном напоре через донное отверстие сосуда.
sdh = Qdt; sdh = m so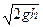
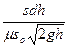
где h – переменная высота уровня жидкости;
dh – изменение высоты жидкости за время dt.
Рис. Схема опорожнения сосуда
Найдем время полного опорожнения сосуда, проинтегрировав выражение dt = f (h):
T =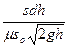
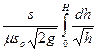
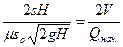
Вывод: время полного опорожнения сосуда в два раза больше, чем время истечения того же объема жидкости при постоянном напоре Н, равном первоначальному.
2.7. Кавитация в потоке жидкости
2.7.1. Физика явления
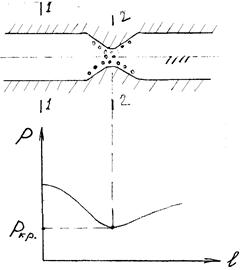
Рассмотрим трубу, имеющую зауженный участок.
Запишем уравнение Бернулли в давлениях для сечений 1-1 и 2-2, приняв за плоскость сравнения ось трубы:
Кавитацией называется нарушение сплошности потока жидкости вследствие образования в ней пустот (пузырьков, пузырей, полостей), заполненных паром или газом. При снижении давления до давления насыщенного пара из жидкости выделяются ее пары и растворенные в ней газы. Сначала образуются кавитационные пузырьки, которые при заполнении их газами и парами растут. Они перемещаются потоком жидкости, увеличиваются в размерах, образуют круп-ные пузыри и полости.
Для воды при t = 20°С рн.п. = 2400 Па (для сравнения ратм = 101320 Па).
Кавитация – это холодное «кипение» жидкости. За зоной кавитации давление растет, рост пузырей прекращается и они мгновенно «схлопываются».
Запишем уравнение Бернулли в напорах для двух произвольных сечений потока реальной жидкости:
Из уравнения видно, что снижение давления может произойти не только при увеличении скорости движения жидкости, но и по другим причинам. Например. при значительном увеличении геометрической высоты (при чрезмерном поднятии трубопровода), при больших потерях напора (если на трубопроводе много местных сопротивлений), что также может привести к кавитации.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет