рис интеграле что это такое
Ингредиенты Рис каша интеграле
Пищевая ценность и химический состав «Рис каша интеграле».
| Нутриент | Количество | Норма** | % от нормы в 100 г | % от нормы в 100 ккал | 100% нормы |
| Калорийность | 116.7 кКал | 1684 кКал | 6.9% | 5.9% | 1443 г |
| Белки | 2.5 г | 76 г | 3.3% | 2.8% | 3040 г |
| Жиры | 0.5 г | 56 г | 0.9% | 0.8% | 11200 г |
| Углеводы | 25.7 г | 219 г | 11.7% | 10% | 852 г |
| Вода | 71.3 г | 2273 г | 3.1% | 2.7% | 3188 г |
| Макроэлементы | |||||
| Кальций, Ca | 3 мг | 1000 мг | 0.3% | 0.3% | 33333 г |
| Магний, Mg | 0.67 мг | 400 мг | 0.2% | 0.2% | 59701 г |
| Натрий, Na | 0.6 мг | 1300 мг | 216667 г | ||
| Сера, S | 0.67 мг | 1000 мг | 0.1% | 0.1% | 149254 г |
| Хлор, Cl | 0.93 мг | 2300 мг | 247312 г | ||
| Микроэлементы | |||||
| Железо, Fe | 0.001 мг | 18 мг | 1800000 г | ||
| Марганец, Mn | 0.0011 мг | 2 мг | 0.1% | 0.1% | 181818 г |
| Медь, Cu | 0.4 мкг | 1000 мкг | 250000 г | ||
| Молибден, Mo | 1.067 мкг | 70 мкг | 1.5% | 1.3% | 6560 г |
| Фтор, F | 66.67 мкг | 4000 мкг | 1.7% | 1.5% | 6000 г |
Энергетическая ценность Рис каша интеграле составляет 116,7 кКал.
Основной источник: Создан в приложении пользователем. Подробнее.
** В данной таблице указаны средние нормы витаминов и минералов для взрослого человека. Если вы хотите узнать нормы с учетом вашего пола, возраста и других факторов, тогда воспользуйтесь приложением «Мой здоровый рацион».
Новое тесто Integrale во всех ресторанах il FORNO!
Теперь во всех ресторанах il FORNO можно заказать пиццу, пасту и фокаччу не только на обычном, ржаном или безглютеновом тесте, но и на особом итальянском тесте Integrale (Интеграле).
Это не только вкусно, но ещё и отличная альтернатива для гостей, особенно тщательно следящих за рационом и пользой каждого ингредиента.
Тесто замешивается на основе одноимённой муки грубого помола, которая получается путём перемола всего зерна пшеницы вместе с оболочкой, в которой содержатся клетчатка, витамины B и E, минералы и микроэлементы (железо, марганец, селен, хром, фтор, кальций, медь, цинк, калий, магний) и белки.
В отличие от белой муки, которая содержит только внутреннюю часть зерна (крахмал), цельнозерновая мука считается более полезной. Она нормализует работу пищеварительного тракта, не провоцирует повышение холестерина или скачки сахара за счёт низкого гликемического индекса, медленно усваивается, а значит Integrale полезно даже для тех, кто сидит на диете и стремится сбросить лишний вес.
Рестораны il FORNO
www.ilforno.ru
Средний чек – 2500 руб
Кутузовский проспект, 2/1, стр.6
ул. Остоженка, 3/14, Москва
ул. Неглинная, 8/10
Сегодня вы поймёте, что такое интеграл в математике
(и в программировании)
Недавно мы разобрали, что такое знаки Σ и П в математике — это операции, которые, по сути, похожи на циклы в программировании. В одном случае мы складывали много чисел по определённому принципу, а в другом — умножали.
Сегодня посмотрим на интеграл ∫ — что это такое и какой цикл можно сделать из него.
Но сначала: что такое функция
Интегралы в математике всегда связаны с функциями, поэтому сначала поговорим про них.
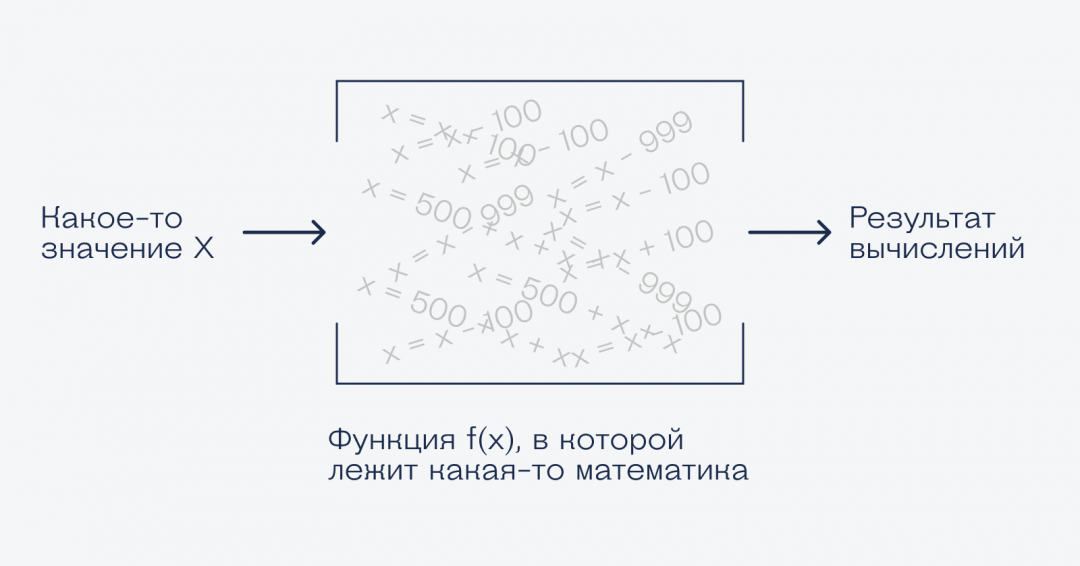
Функцию можно представить как «коробку с математикой». У тебя есть какая-то масса математических операций, ты их «запаковываешь» в функцию. Теперь ты можешь эту массу операций вызывать в своих математических выражениях одним действием.
У функции есть один или несколько аргументов — это те числа, к которым нужно применить массу математических операций. Можно представим, что мы засунули это число в коробку с математикой, потрясли и получили на выходе другое число.
Если посчитать f(x) для одного числа, получится другое число. Если посчитать f(x) от 100 чисел, получится 100 других чисел. А если непрерывно считать f(x) для бесконечного количества чисел, то получится бесконечное количество других чисел.
Что такое интеграл
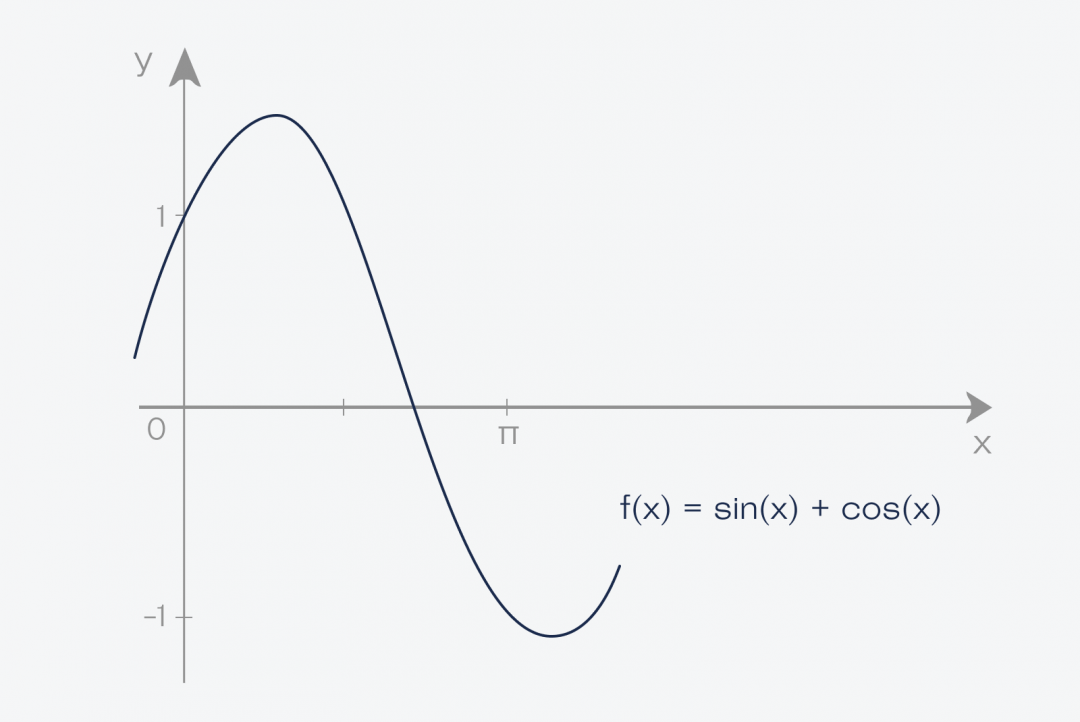
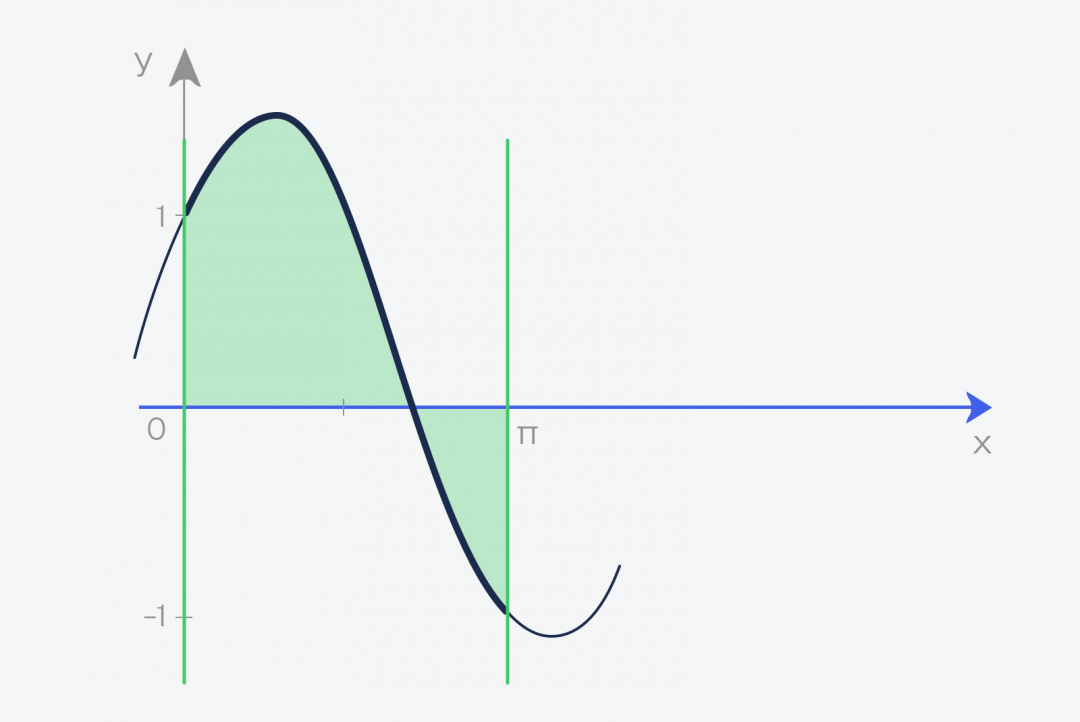
Итак, у нас есть некая функция, у неё есть числа на входе и числа на выходе. Эти пары чисел можно использовать для построения графика функции.
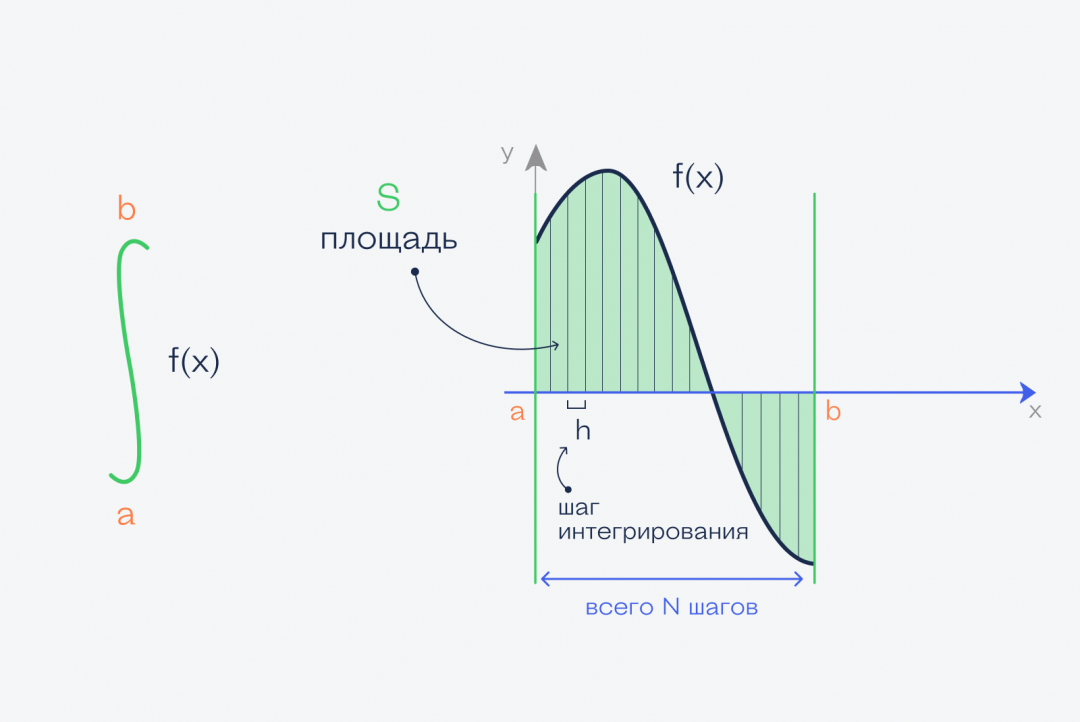
Теперь берём этот график функции и проводим две линии, которые ограничивают график. Получается фигура, которая сверху зависит от нашей функции, а с остальных сторон ограничена прямыми линиями и осью:
А теперь то, ради чего всё это затевалось:
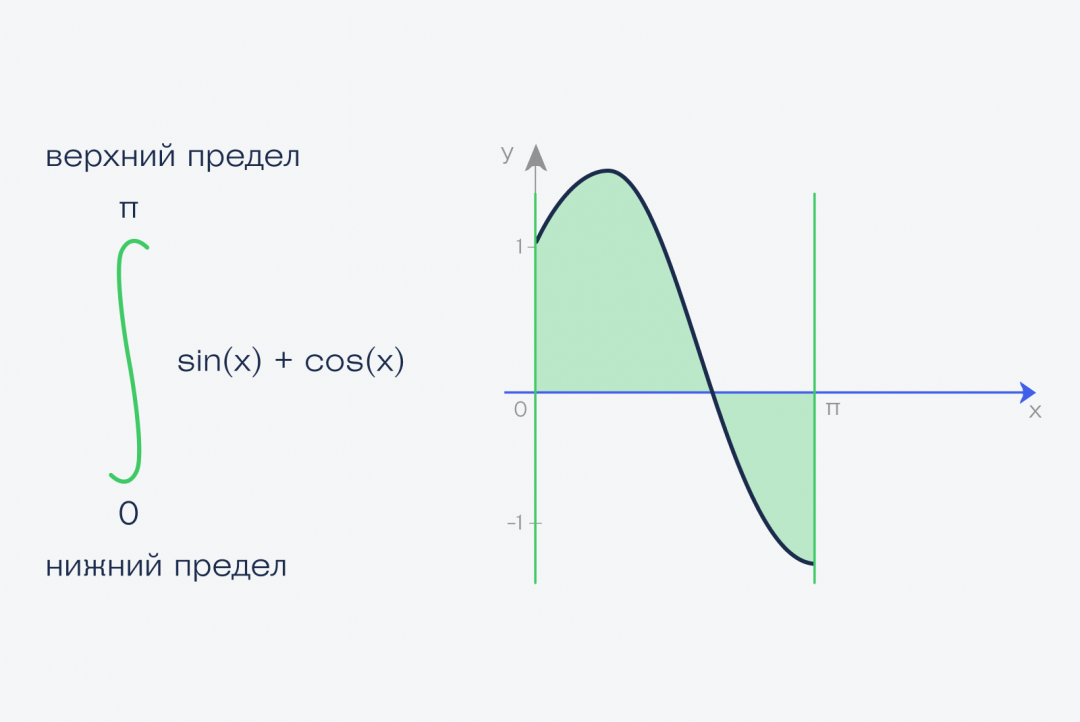
✅ Площадь этой фигуры и есть интеграл функции f(x) = sin(x) + cos(x) на отрезке от a до b
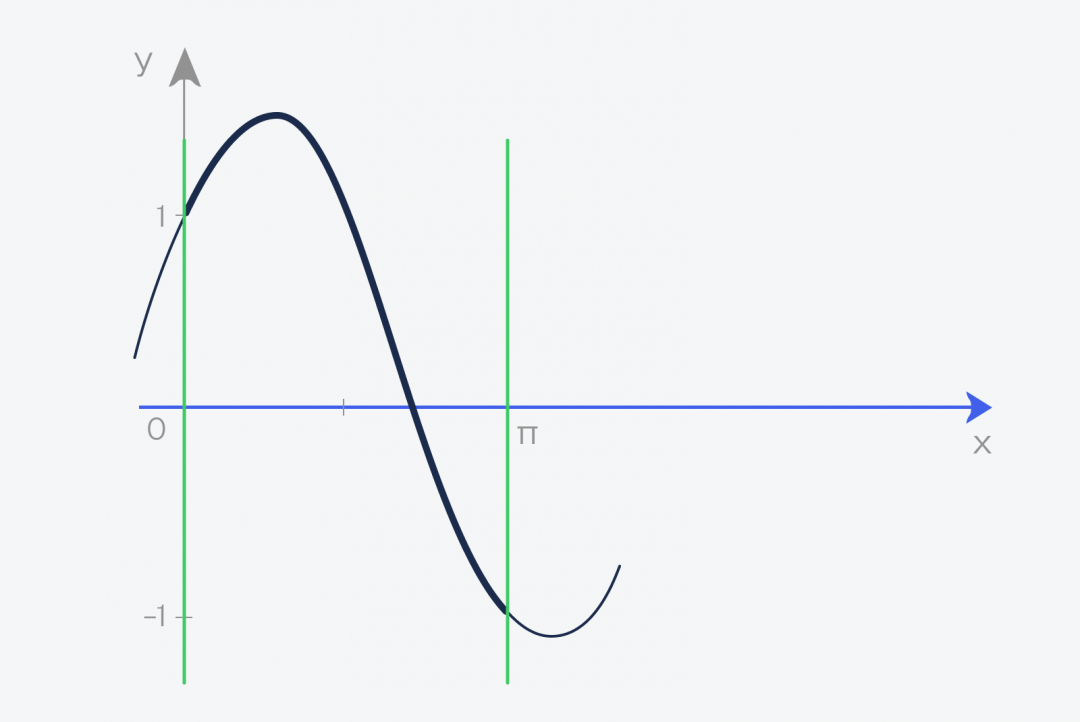
В нашем случае мы считаем интеграл от нуля до числа пи — 3,1415926.
Это называется определённый интеграл. Определённый — это когда у нас определены начало и конец фигуры — в математике это называют пределами интегрирования. Записывается этот интеграл так:
В математике есть ещё неопределённые интегралы, у которых нет пределов интегрирования. Ими мы заниматься не будем, потому что ответом к неопределённому интегралу будет не конкретное число, а формула.
Зачем нужны интегралы в народном хозяйстве
Вы удивитесь, но в первую очередь интегралы нужны, чтобы находить площади и объёмы. В буквальном смысле: вот фигура, вот её описание в виде функции, проинтегрировали — узнали площадь. Будете, например, заливать бетоном красивую кривую дорожку — узнаете, сколько вам нужно бетона.
Интегралы нужны в математике и физике, это один из инструментов вычислений.
Если вы астрофизик, интеграл поможет вам рассчитать какие-нибудь свойства звёзд с течением времени. А математики говорят, что в интегралах не нужно искать практический смысл; их нужно любить, как мать, и почитать, как отца.
Как посчитать интеграл (то есть найти площадь)
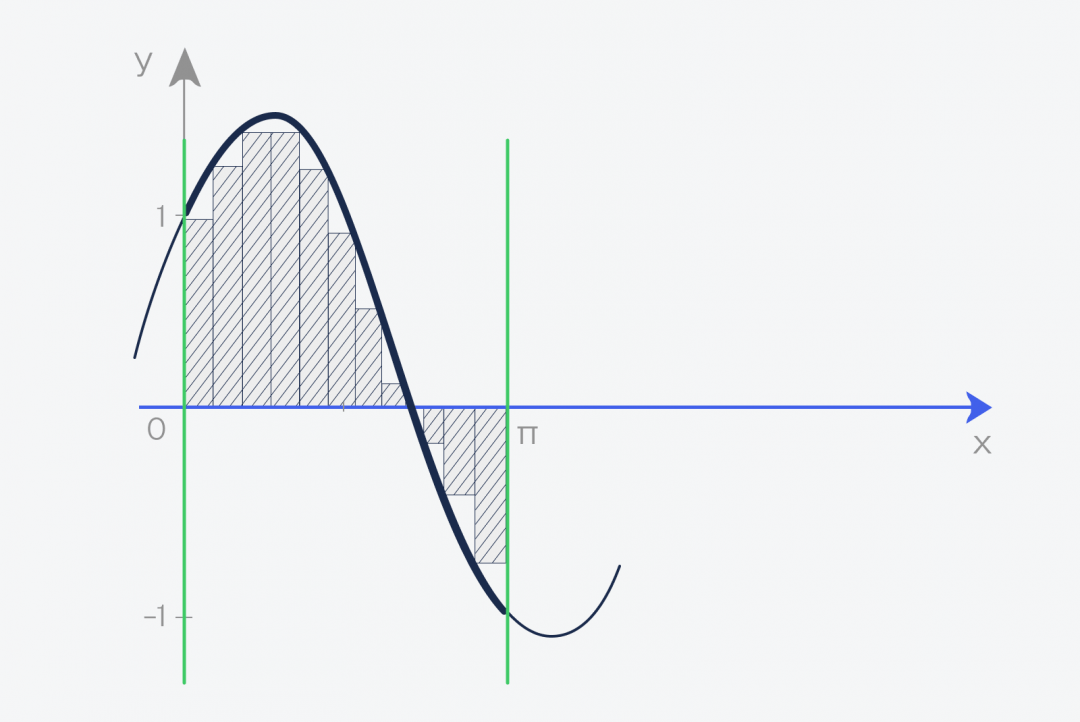
Если бы у нас был прямоугольник, то всё просто: перемножаем высоту на ширину. Если бы была трапеция, тоже ещё как-то что-то можно. Но сверху у нас кривая, поэтому так сделать не получится. Решение придумали такое:
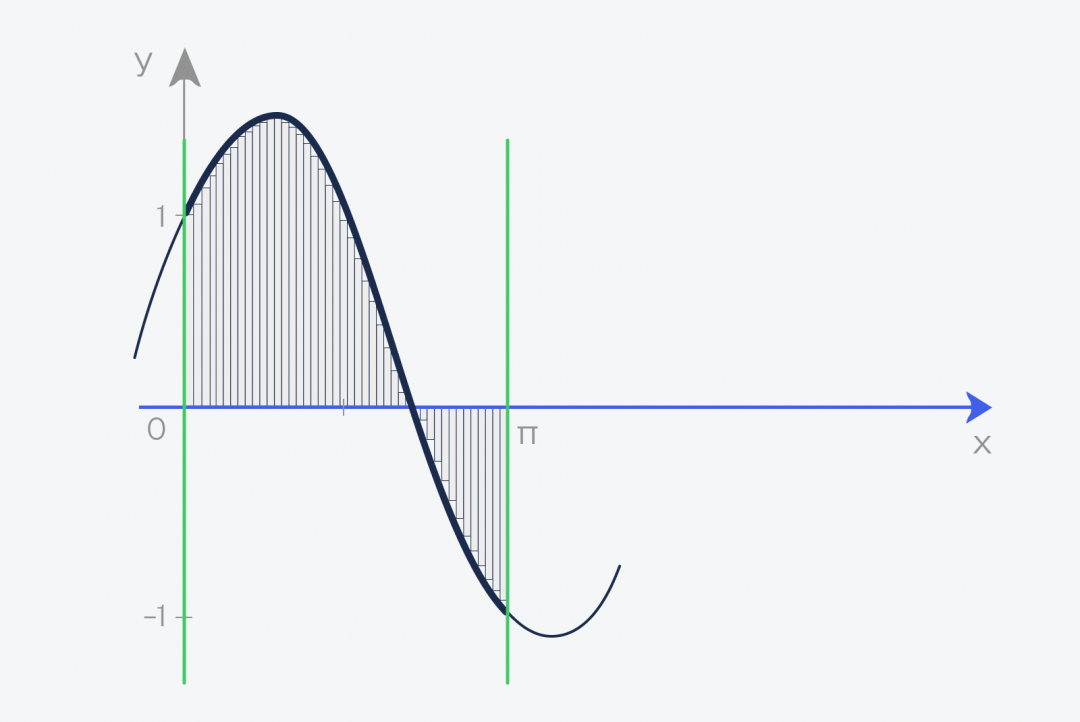
Минус такого подхода в том, что, как бы мы ни старались, прямоугольники не могут повторить все изгибы, и появится погрешность. С другой стороны, чем тоньше будут эти прямоугольники, тем точнее будет ответ. Получается, что наша задача — нарезать фигуру как можно тоньше.
Теперь задача становится намного проще: мы просто считаем площадь каждого прямоугольника и складываем их вместе. В таком виде задачу уже можно решить простым алгоритмом.
Пишем код
Раз нам нужно разбить интервал на много частей а потом с каждой из них сделать одно и то же, то это точно задача для цикла. Для этого нам понадобится шаг цикла — какой ширины будут наши прямоугольники, чтобы бы могли их одинаково перебирать.
Чтобы посчитать шаг, находим расстояние между конечной и начальной точкой и делим на желаемое количество прямоугольников (это будет нашей точностью интегрирования).
Общая логика работы будет такая:
На картинке — все исходные данные, а ниже — код, который считает интеграл. Смотрите на картинку и читайте комментарии: так будет ещё проще разобраться в коде:
Что дальше
Теперь этот код можно изменить так, чтобы он считал интеграл в любых пределах у любой функции. С точки зрения математики это не самый точный результат, но всё зависит от того, сколько точных знаков после запятой нам нужно.
В следующей серии продолжим разбираться со страшной математикой. Если есть пожелания для разбора — напишите в комментариях.
Рис бурый Интеграле PREMIUM «Националь», 500 г
| Белки: | 7,5 г/100 г |
| Жиры: | 1 г/100 г |
| Углеводы: | 79 г/100 г |
| Калорийность: | 350 ккал/100 г |
| Вес нетто: | 500 г |
| Упаковка: | п/пакет |
| Срок хранения: | 12 мес. |
| Производитель: | ООО Компания «Ангстрем Трейдинг» |
| Страна производитель: | Россия |
| Торговая марка: | Националь |
Описание
Рис Интеграле Националь Премиум – итальянский сорт бурого риса.
Не подвергается шлифовке, поэтому в его зёрнах максимально сохраняется клетчатка, полезные пищевые волокна и витамины.
Содержит медленные углеводы, которые надолго дарят чувство сытости и заряжают энергией.
Идеален для диетического питания.
Рецепт приготовления вкусного риса с изюмом и яблоками.
Первым делом необходимо заняться изюмом, поскольку он должен постоять в горячей воде около 1-2 часов.
Теперь переходите к приготовлению ароматного риса. Для этого промойте рис несколько раз под холодной водой и только потом варите.
Сразу же добавьте все специи, чтобы они успели передать свой пряный аромат рису.
К рису прекрасно подойдут яблоки.
Очистите яблоки от кожуры и нарежьте их на небольшие кусочки.
Соедините рис с яблоками, подержите под крышкой минут десять и подавайте к столу.
Готовое блюдо можно украсить свежими фруктами, медом или любой другой добавкой на ваш вкус.
Интегралы для чайников: как решать, правила вычисления, объяснение
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие « интеграл »
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
Свойства определенного интеграла
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.