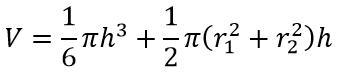Что такое шаровой сектор

Шаровой сектор

Смотреть что такое «Шаровой сектор» в других словарях:

Шаровой сектор — 1 го рода … Википедия

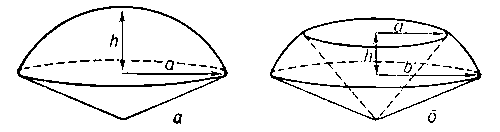
ШАРОВОЙ СЕКТОР — геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов (шаровой сектор 1 го рода) или вокруг диаметра, не пересекающего его дуги (шаровой сектор 2 го рода); объем шарового сектора (1 го и 2 го рода):;полная… … Большой Энциклопедический словарь

шаровой сектор — геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов (шаровой сектор 1 го рода рис. а) или вокруг диаметра, не пересекающего его дуги (шаровой сектор 2 го рода рис. б); объём шарового сектора (1 го и 2 го рода) V … Энциклопедический словарь

ШАРОВОЙ СЕКТОР — геом. тело, возникающее при вращении сектора вокруг одного из его радиусов (Ш. с. 1 го рода рис. а) или вокруг диаметра, не пересекающего его дуги (Ш. с. 2 го рода рис. б); объём Ш.с. (1 го и 2 го рода) V= 2/3ПИ*R2h; полная поверхность Ш. с. 1 го … Естествознание. Энциклопедический словарь

Сектор (в математике) — Сектор в математике, 1) С. на плоскости плоская фигура, ограниченная двумя полупрямыми, исходящими из внутренней точки фигуры, и дугой контура. С. круга фигура, ограниченная двумя радиусами и дугой, на которую они опираются. Площадь С. круга… … Большая советская энциклопедия

СЕКТОР — (1) круговой часть круга, ограниченная двумя радиусами и дугой круга; (2) плоской фигуры часть этой фигуры, ограниченная двумя лучами, исходящими из внутренней точки, и дугой контура; (3) пространственной фигуры часть этой фигуры, ограниченная… … Большая политехническая энциклопедия

Сектор — В Викисловаре есть статья «сектор» Сектор: Сектор в геометрии часть круга, ограниченная двумя ради … Википедия

Сектор (геометрия) — У этого термина существуют и другие значения, см. Сектор. Сектор круга закрашен зелёным Сектор в геометрии часть круга, ограниченная дугой и двумя ра … Википедия

Сектор — I Сектор (позднелатинский sector, от лат. seco разрезаю, разделяю) 1) четко выделенная составная часть. 2) Участок, ограниченный радиальными линиями, например С. стадиона, С. наблюдения, С. обстрела. 3) Часть народного… … Большая советская энциклопедия

СЕКТОР — 1) С. н а п л о с к о с т и плоская фигура, ограниченная двумя полупрямыми, исходящими из внутренней точки фигуры, и дугой контура. С. круга (к р у г о в о й с е к т о р) фигура, ограниченная двумя радиусами и дугой, на к рую они опираются.… … Математическая энциклопедия

Источник

Шаровой сегмент, сектор и слой

Шаровой сегмент

Шаровой сегмент — это меньшая часть шара, отсекаемая от него плоскостью, не проходящей через центр шара.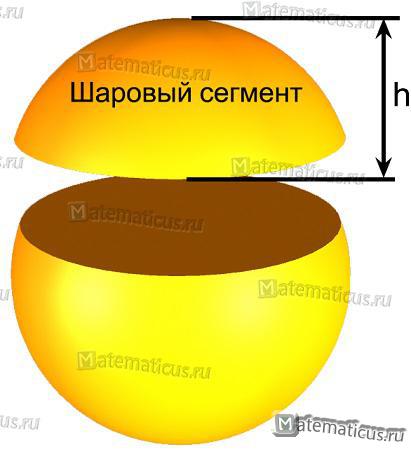

h – высота шарового сегмента
Формула объёма шарового сегмента: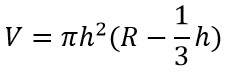

Формула площади поверхности сферического сегмента:

S=2 π Rh = π (R 2 +h 2 ) = 2 π R 2 (1-cos α )

α – зенитный угол
R — радиус шара

Шаровой слой

Шаровой слой — часть шара, заключенная между двумя параллельными секущими плоскостями.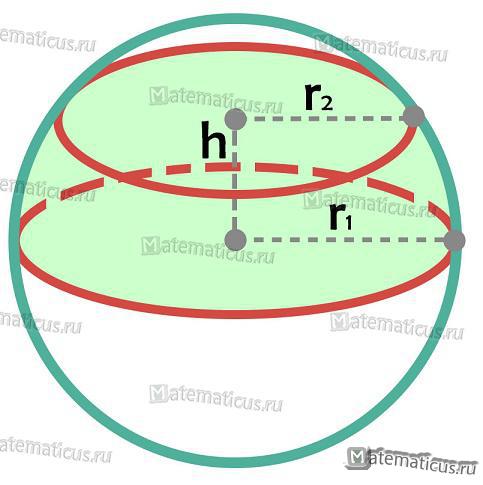

Формула поверхности шарового слоя:

S=2 π Rh

Формула объёма шарового слоя:

Шаровой сектор

Шаровой сектор — это фигура вращения кругового сектора вокруг прямой, содержащей радиус, ограничивающий сектор.


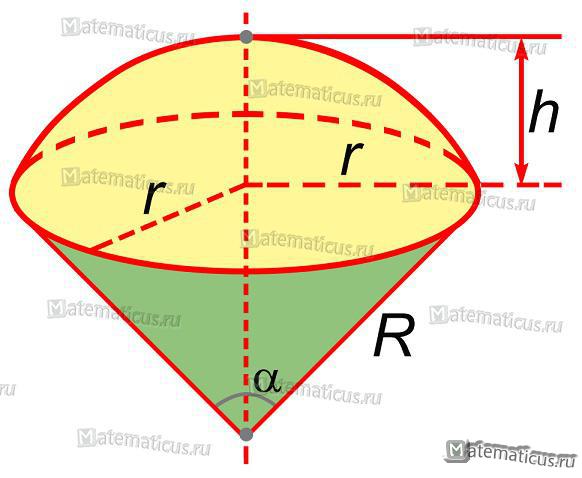
Формула площади шарового сектора:

S= π R(r+2h)

Формула объёма шарового сектора: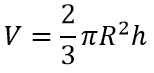


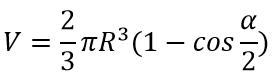
где α – угол между осью и образующей конуса
См. также
Сфера, полусфера

Источник

Шаровой сектор

Свойства

См. также

Примечания

Полезное

Смотреть что такое «Шаровой сектор» в других словарях:

ШАРОВОЙ СЕКТОР — геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов (шаровой сектор 1 го рода) или вокруг диаметра, не пересекающего его дуги (шаровой сектор 2 го рода); объем шарового сектора (1 го и 2 го рода):;полная… … Большой Энциклопедический словарь

шаровой сектор — геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов (шаровой сектор 1 го рода рис. а) или вокруг диаметра, не пересекающего его дуги (шаровой сектор 2 го рода рис. б); объём шарового сектора (1 го и 2 го рода) V … Энциклопедический словарь

ШАРОВОЙ СЕКТОР — геом. тело, возникающее при вращении сектора вокруг одного из его радиусов (Ш. с. 1 го рода рис. а) или вокруг диаметра, не пересекающего его дуги (Ш. с. 2 го рода рис. б); объём Ш.с. (1 го и 2 го рода) V= 2/3ПИ*R2h; полная поверхность Ш. с. 1 го … Естествознание. Энциклопедический словарь

Сектор (в математике) — Сектор в математике, 1) С. на плоскости плоская фигура, ограниченная двумя полупрямыми, исходящими из внутренней точки фигуры, и дугой контура. С. круга фигура, ограниченная двумя радиусами и дугой, на которую они опираются. Площадь С. круга… … Большая советская энциклопедия

СЕКТОР — (1) круговой часть круга, ограниченная двумя радиусами и дугой круга; (2) плоской фигуры часть этой фигуры, ограниченная двумя лучами, исходящими из внутренней точки, и дугой контура; (3) пространственной фигуры часть этой фигуры, ограниченная… … Большая политехническая энциклопедия

Сектор — В Викисловаре есть статья «сектор» Сектор: Сектор в геометрии часть круга, ограниченная двумя ради … Википедия

Сектор (геометрия) — У этого термина существуют и другие значения, см. Сектор. Сектор круга закрашен зелёным Сектор в геометрии часть круга, ограниченная дугой и двумя ра … Википедия

Сектор — I Сектор (позднелатинский sector, от лат. seco разрезаю, разделяю) 1) четко выделенная составная часть. 2) Участок, ограниченный радиальными линиями, например С. стадиона, С. наблюдения, С. обстрела. 3) Часть народного… … Большая советская энциклопедия

СЕКТОР — 1) С. н а п л о с к о с т и плоская фигура, ограниченная двумя полупрямыми, исходящими из внутренней точки фигуры, и дугой контура. С. круга (к р у г о в о й с е к т о р) фигура, ограниченная двумя радиусами и дугой, на к рую они опираются.… … Математическая энциклопедия

Источник

Что такое шаровой сектор

Объём шара радиуса R равен 4 / 3 π R 3

Шаровой сегмент. Объём шарового сегмента.

Шаровой сегмент – это часть шара, которая осекается плоскостью от шара.

Шаровой слой. Объём шарового слоя.

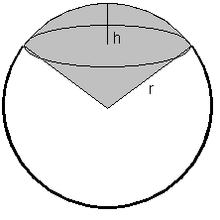
Шаровой сектор. Объём шарового сектора.

Объем шарового сектора можно найти по формуле:

Источник

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок №14. Объем шара и его частей

Перечень вопросов, рассматриваемых в теме

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10-11 учебник для общеобразов. учрежд.: база и профильн. М: Просвещение.2009

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни и др. – М.: Просвещение, 2014. – 255, сс. 121-126.

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.

Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.

Радиусом шара называют всякий отрезок, соединяющий центр шара с точкой шаровой поверхности.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.

Концы любого диаметра шара называются диаметрально противоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара.

Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями

Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями

Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость.

Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.

Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы

Объем шара равен .

Объем шарового сегмента равен .

Объем шарового сектора равен .

Объем шарового слоя равен .

Примеры и разбор решения заданий тренировочного модуля

№1. Круговой сектор радиуса R с центральным углом 60 градусов вращается вокруг одного из радиусов, образующих этот угол. Найдите объем тела вращения.

№2. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара.

Решение: запишем формулу для вычисления объема шарового слоя.

Чтобы найти объём шарового слоя нам необходимо знать его высоту и радиусы двух его оснований.

По условию задачи нам дано расстояние между сечениями, как раз-таки это расстояние и есть высота данного шарового слоя, и она равна .

Теперь найдём чему равны радиусы оснований шарового слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга вычисляется по формуле . Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания равен (см), радиус второго основания равен (см).

Подставим радиусы оснований и высоту шарового слоя в формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен .

Источник