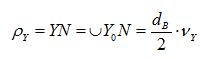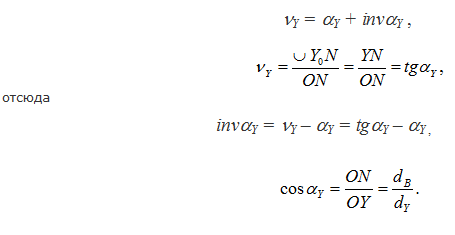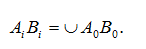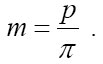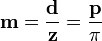Что такое эвольвента зубчатого колеса

Что такое эвольвента зубчатого колеса

Для параметров зубчатого колеса справедливы следующие соотношения

— диаметр окружности произвольного радиуса,

— диаметр делительной окружности,

— шаг по окружности произвольного радиуса,

— шаг по делительной окружности,

В зависимости от соотношения между толщиной зуба и шириной впадины на делительной окружности зубчатые колеса делятся на:

Более подробно познакомиться с основными определениями и расчетными зависимостями можно в литературе [ 11.1 ] и в ГОСТ 16530-83.

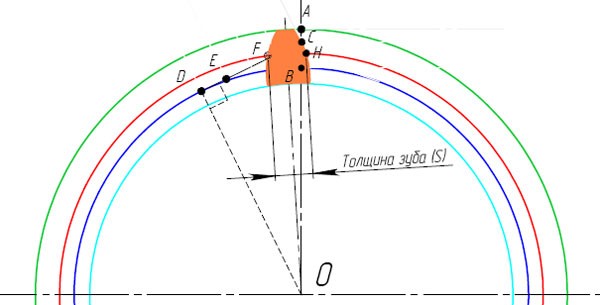
Толщина зуба колеса по окружности произвольного радиуса .

Толщина зуба по дуге делительной окружности

Угловая толщина зуба по окружности произвольного радиуса из схемы на рис. 12.2

Подставляя в формулу угловой толщины эти зависимости, получим

Методы изготовления эвольвентных зубчатых колес .

Существует множество вариантов изготовления зубчатых колес. В их основу положены два принципиально отличных метода:

Из вариантов изготовления по способу копирования можно отметить:

Из вариантов изготовления по способу огибания наибольшее распространение имеют:

Для сокращения номенклатуры режущего инструмента стандарт устанавливает нормативный ряд модулей и определенные соотношения между размерами элементов зуба. Эти соотношения определяются:

По ГОСТ 13755-81 значения параметров исходного контура должны быть следующими:

Исходный производящий контур отличается от исходного высотой зуба h 0 = 2.5m.

Станочным зацеплением называется зацепление, образованное заготовкой колеса и инструментом, при изготовлении зубчатого колеса на зубообрабатывающем оборудовании по способу обката. Схема станочного зацепления колеса и инструмента с производящим контуром, совпадающим с исходным производящим контуром, изображена на рис. 12.4.

Основные размеры зубчатого колеса .

Определим основные размеры эвольвентного зубчатого колеса, используя схему станочного зацепления (рис. 12.4).

Так как стночно-начальная прямая перекатывается в процессе огибания по делительной окружности без скольжения, то дуга s-s по делительной окружности колеса равна ширине впадины e-e по станочно-начальной прямой инструмента. Тогда, c учетом схемы на рис. 12.5, можно записать

Виды зубчатых колес (Классификация по величине смещения) .

В зависимости от расположения исходного производящего контура относительно заготовки зубчатого колеса, зубчатые колеса делятся на нулевые или без смещения, положительные или с положительным смещением, отрицательные или с отрицательным смещением.

Подрезание и заострение зубчатого колеса .

На рис. 12.7 изображены два эвольвентных зуба для которых

Для термобработанных зубчатых колес с высокой поверхностной прочностью зуба заострение вершины зуба является нежелательным. Термообработка зубьев (азотирова-ние, цементация, цианирование), обеспечивающая высо Рис. 12.7 кую поверхностную прочность и твердость зубьев при сохранении вязкой серцевины, осуществляется за счет насыщения поверхностных слоев углеродом. Вершины зубьев, как выступающие элементы колеса, насыщаются углеродом больше. Поэтому после закалки они становятся более твердыми и хрупкими. У заостренных зубьев появляется склонность к скалыванию зубьев на вершинах. Поэтому рекомендуется при изготовлении не допускать толщин зубьев меньших некоторых допустимых значений. То есть заостренным считается зуб у которого

При этом удобнее пользоваться относительными величинами [s a /m ]. Обычно принимают следующие допустимые значения

улучшение, нормализация [s a /m ] = 0.2;

цианирование, азотирование [s a /m ] = 0.25. 0.3;

цементация [s a /m ] = 0.35. 0.4.

Подрезание эвольвентных зубьев в станочном зацеплении

Источник

iSopromat.ru

Эвольвентное зацепление зубчатых колес удовлетворяет основному закону зацепления, обеспечивает постоянство передаточного отношения, допускает отклонение межосевого расстояния зубчатых передач и точно стандартизируется.

Подавляющее большинство зубчатых передач, применяемых в технике, имеет зубчатые колеса с эвольвентным профилем.

Эвольвента как кривая для формирования профиля зуба была предложена Л. Эйлером. Она обладает значительными преимуществами перед другими кривыми, применяемыми для этой цели, – удовлетворяет основному закону зацепления, обеспечивает постоянство передаточного отношения, нечувствительна к неточностям межосевого расстояния (что облегчает сборку), наиболее проста и технологична в изготовлении, легко стандартизируется (что особенно важно для такого распространенного вида механизмов как зубчатые передачи).

На следующем видео показан пример эвольвентного зацепления зубчатых колес

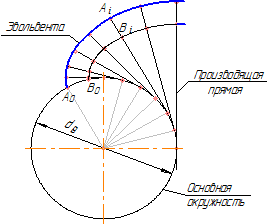
Эвольвента – это траектория движения точки, принадлежащей прямой, перекатывающейся без скольжения по окружности. Данная прямая называется производящей прямой, а окружность, по которой она перекатывается – основной окружностью (рисунок 38 а).

Эвольвента обладает следующими свойствами, которые используются в теории зацепления:

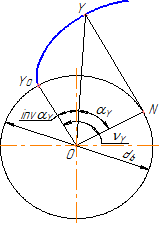
Положение любой точки на эвольвенте может быть однозначно охарактеризовано диаметром окружности, на которой она расположена, а также характерными для эвольвенты углами: углом развернутости (обозначается ν ), углом профиля ( α ), эвольвентным углом – inv α (рисунок 38 б). На рисунке 38 б показаны эти углы для произвольно выбранной на эвольвенте точки Y, поэтому они имеют соответствующий индекс:

То есть индекс показывает, на какой окружности находится рассматриваемая точка эвольвенты, поэтому для характерных окружностей используются индексы, приведенные выше.

Например: α _a1 – угол профиля эвольвенты в точке, лежащей на окружности вершин первого колеса;
inv α – эвольвентный угол в точке эвольвенты, находящейся на делительной окружности колеса и т.д.

Рассмотрим свойства эвольвенты. Первое свойство имеет строгое математическое доказательство, однако в рамках данного короткого курса оно не приводится.

Так как при формировании эвольвенты производящая прямая перекатывается по основной окружности без скольжения, то в данный момент времени она вращается вокруг точки N (N – мгновенный центр скоростей), описывая бесконечно малую дугу окружности, которая и определяет кривизну эвольвенты в данной точке. Т.е. отрезок NY – это радиус кривизны эвольвенты в точке Y (NY= ρ _Y).

Но отрезок NY в точности равен дуге NY₀ (это та же дуга только вытянутая в прямую линию). Таким образом, имеем:

Чем больше радиус основной окружности, тем больше радиус кривизны эвольвенты в любой ее точке (то есть форма эвольвенты действительно определяется величиной радиуса основной окружности).

Второе свойство также легко просматривается. Так как N – мгновенный центр скоростей, то скорость точки Y перпендикулярна радиусу NY. Но скорость точки, движущейся по криволинейной траектории, направлена по касательной к этой траектории – в данном случае по касательной к эвольвенте в точке Y.

Перпендикуляр к касательной – есть нормаль, поэтому прямая YN с одной стороны является нормалью к эвольвенте в точке Y, с другой стороны является касательной к основной окружности (как производящая прямая, перекатывающаяся по основной окружности).

То, что точка N является центром кривизны эвольвенты в точке Y, показано при рассмотрении первого свойства. Запишем некоторые зависимости, которые используются в дальнейшем при изучении геометрии эвольвентного зацепления (получаются из рассмотрения рисунка 38 б):

Третье свойство эвольвенты очевидно из рисунка 38а. Действительно, если на производящей прямой взять две точки (А и В), то они будут описывать две совершенно одинаковых эвольвенты, причем, как бы не перемещалась производящая прямая, расстояние между этими точками не изменяется (A_iB_i = Const). Т.е. действительно это эквидистантные (равноотстоящие друг от друга) кривые. Но, самое важное, что это расстояние A_iB_i равно расстоянию между этими эвольвентами, измеренному по дуге основной окружности:

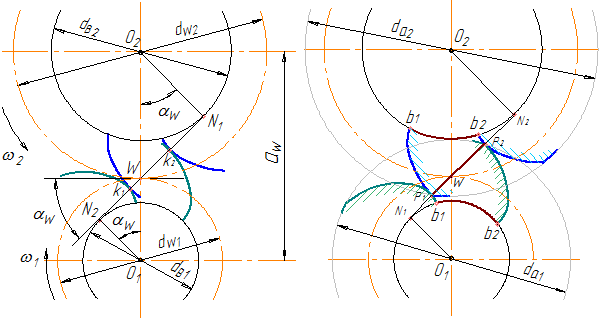
Признаком того, что два криволинейных профиля касаются (а не пересекаются), является наличие у них в точке контакта общей нормали. В связи с этим контакт двух эвольвентных профилей происходит на общей касательной к основным окружностям N₁N₂ (рисунок 39), которая одновременно будет являться общей нормалью к этим профилям в точке их касания в любой момент времени (на основании второго свойства эвольвенты).

Геометрическое место точек контакта профилей, которое они занимают в процессе работы пары зубьев, называется линией зацепления. Таким образом, в эвольвентной передаче линией зацепления является прямая N₁N₂ (общая касательная к основным окружностям).

На рисунке 39 а показано зацепление двух эвольвентных профилей в разные моменты времени. В обоих положениях прямая N₁N₂ является общей нормалью к этим касающимся профилям и проходит через полюс зацепления W (мгновенный центр относительного вращения).

Это, с одной стороны показывает, что эвольвентные профили удовлетворяют основному закону зацепления, с другой стороны обеспечивают постоянство передаточного отношения, т.к. полюс зацепления не меняет своего положения в процессе работы пары (отношение O₂W/O₁W остается постянным).

С изменением межосевого расстояния будет меняться только положение линии зацепления, но вся картина зацепления останется такой же, т.е. по-прежнему будет сохраняться основной закон зацепления, величина и постоянство передаточного отношения. Это очень важное свойство эвольвентного зацепления, т.к. позволяет вписывать передачу в разные межосевые расстояния, что особенно важно при проектировании коробок скоростей, планетарных и дифференциальных механизмов.

Передача оказывается малочувствительной к неточностям межосевого расстояния, что позволяет снизить требования к точности сборки.

Отрезок N₁N₂ называется теоретической линией зацепления. На этом участке происходит нормальная работа двух неограниченных эвольвент.

В реальной передаче эвольвенты ограничены («обрезаны») окружностями вершин, поэтому вся работа пары происходит на участке линии зацепления P₁P₂, заключенном между окружностями вершин (рисунок 39б).

Отрезок P₁P₂ называется рабочей (активной) частью линии зацепления (иногда называют просто «рабочая линия зацепления», или «активная линия зацепления»). На рисунке 39б показано два положения одной и той же пары: в начале зацепления (зуб ведомого колеса работает своей вершиной, зуб ведущего колеса – нижней рабочей точкой профиля Р₁), и в конце зацепления (зуб ведущего колеса работает своей вершиной и в следующий момент выйдет из зацепления, зуб ведомого колеса работает своей нижней рабочей точкой профиля Р₂).

Примечание: здесь термин «нижняя» или «верхняя» точка относится к положению точек относительно основной окружности, независимо от того, как эти точки располагаются одна относительно другой в пространстве. Из двух рассматриваемых точек профиля «нижней» будет та, которая располагается ближе к основной окружности.

При увеличении радиуса основной окружности до бесконечности радиус кривизны эвольвенты в любой ее точке также становится бесконечно большим, т.е. основная окружность и эвольвента превращаются в прямые линии. Эвольвентное зубчатое колесо превращается в зубчатую рейку с прямолинейным профилем зуба.

Таким образом, рейка с прямолинейным профилем зуба представляет собой частный случай эвольвентного зубчатого колеса и обладает всеми его свойствами, т.е. может работать с любым эвольвентным колесом (при одном и том же модуле) без нарушения основного закона зацепления. При этом вращательное движение колеса преобразуется в поступательное движение рейки или поступательное движение рейки преобразуется во вращательное движение колеса с соблюдением постоянства передаточного отношения.

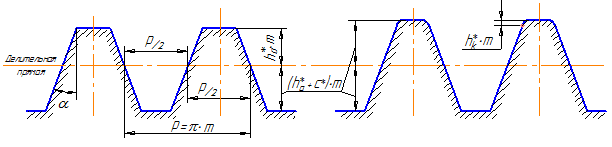
Т.к. зубчатая рейка с прямолинейным профилем зуба с одной стороны имеет простые формы и легко задать размеры ее элементов, с другой стороны представляет собой эвольвентное зубчатое колесо, то ее параметры положены в основу стандартизации эвольвентных зубчатых колес. Стандартная зубчатая рейка называется исходным контуром (рисунок 40а).

Имеется несколько стандартов на исходные контуры, учитывающие специфику некоторых видов передач (мелкомодульных, конических и т.д.). В основном используются параметры, определенные ГОСТ 13 755 – 81.

В соответствии с этим стандартом исходный контур имеет следующие параметры:

Приведенные коэффициенты являются безразмерными величинами. Абсолютное значение какого-либо размера получается умножением соответствующего коэффициента на модуль (Например: высота головки зуба h_a=h_a * ∙m; величина радиального зазора c = c*∙m и т. д.).

Таким образом, форма зуба остается постоянной, а абсолютные размеры определяются модулем (т.е. модуль является как бы коэффициентом пропорциональности).

По высоте зуб исходного контура делится на головку и ножку. Это деление осуществляется делительной прямой. Делительная прямая рейки – это прямая, на которой толщина зуба равна ширине впадины (рисунок 40б).

Высота ножки зуба несколько больше головки для обеспечения радиального зазора между вершинами зубьев одного колеса и окружностью впадин другого после сборки передачи.

Стандартные параметры исходного контура на эвольвентное колесо «переносятся» через делительную окружность (на делительной окружности шаг равен стандартному шагу исходного контура p= π ∙ m, угол профиля равен углу профиля исходного контура α = 20 0 ).

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Эвольвентное зубчатое зацепление

Эвольвентное зацепление – сцепление механических элементов зубчатым способом, в основе которого стоят зубья. Боковины в данном случае выполнены в виде симметрично расположенных эвольвент. Такая форма сцепления позволяет добиться стабильного, беспрерывного передаточного отношения.

Эвольвента – кривая, которой характерен переменный радиус кривизны. Основой такой кривой является точка на прямой, по которой кривая обкатывается без скольжения по окружности. Диаметр образованной окружности выступает основой.

Подобное сцепление значительно превосходит аналоги, так как в отличие от других типов, имеет стабильное сцепление. Впервые было предложено Л. Эйлером. Позволяет избавиться от неточностей межосевых расстояний, что значительно облегчает монтаж. Его также легко стандартизировать и изготовить.

Построение эвольвентного зацепления

Существует несколько способов построения эвольвентного зацепления, используемого для изготовления зубчатых колес, которые можно выполнять вручную или с помощью систем автоматического построения.

При проектировании зацепления зубчатых колес учитывают не только геометрические параметры, но и технологические процесс изготовления, а также желаемые динамические и прочностные показатели готового механизма.

Построение эвольвенты зубчатого колеса состоит из нескольких этапов:

При производстве шестерен зубья несколькими методами: копирования и обкатки. Если необходимо изготовить мелкую деталь, прибегают к методу формообразования, другими словами – горячей накатки. Такой способ менее точен, но форма фрезы при копировании не позволяет выполнить миниатюрные вырезы.

Метод копирования предусматривает вращение фрезы вдоль поверхности, образующее зубья. Она прорезает одну впадину за один проход между соседними зубьями. Затем фреза возвращается в базовое положение с одновременным поворотом заготовки на необходимый угол шага. Такой способ изготовления довольно точный, но производительность его низкая.

Более совершенным способом является метод обкатки. В его основе лежит огибающее движение, соответствующее желаемому движению зубчатого колеса при зацеплении. Процесс производства похож на движение шестерен в работе. Такое зацепление называется станочным. Рабочий инструмент в таком случае изготавливается в виде круглой, зубчатой фрезы или инструментной рейки.

Геометрические параметры

Построенные проекта будущего колеса начинается с расчета его параметров.

Рассмотрим параметры эвольвентного зацепления:

Шаг бывает двух видов:

Модуль — диаметр круга шестерни в миллиметрах, измеряемый к одному зубу. Делится на три вида: начальный (показатель окружности колеса начальной поверхности), основной и делительный (окружность колеса со стандартными значениями модуля и шага).

Число зубьев может быть разное, и зависит от диаметра шестерни, технических параметров и свойств готового механизма. К их параметрам можно отнести:

Угол профиля определяется между определенной точкой зуба, которая лежит на делительной окружности шестерни и вектором, прочерченным к точке от центра круга.

Подобное сцепление используется в различных сферах. Его легко встретить в машиностроении (в коробках передач автомобилей, в строительной, военной, сельскохозяйственной технике, судостроении, гидронасосах, лебедках и часовых механизмах).

На сегодняшний день можно найти множество разновидностей подобных шестерен, которые имеют различные свойства и геометрию. При выборе зубчатых колес в первую очередь нужно обращать внимание на прочность и шумовые характеристики. Особого внимания требует твердость метала, что особо важно для нормальной работы соответствующего механизма.

Источник

Уроки по SolidWorks

Урок посвящен построению зубчатого колеса с эвольвентным профилем зуба. Урок состоит из двух частей. В первой части выложена теория, формулы для расчета и один из способов графического построения эвольвентного профиля зуба.
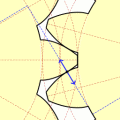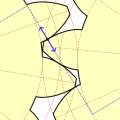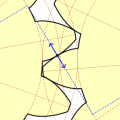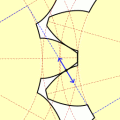
Во второй части (видео) показан способ построения модели зубчатого колеса с использованием графических построений в первой части урока.

*Что такое эвольвента (эволюта)?
*Как построить эвольвенту?
*Как построить зубчатое колесо в программе SolidWorks?
*Формулы для расчета зубчатого колеса?
*Как нарисовать эвольвентный профиль зуба зубчатого колеса?

Итак, начнем с теории.

Параметры зубчатых колёс

Основной теореме зацепления удовлетворяют различные кривые, в том числе эвольвента и окружность, по которым чаще всего изготавливают профили зубьев зубчатого колеса.

В случае, если профиль зуба выполнен по эвольвенте, передача называется эвольвентной.

Для передачи больших усилий с помощью зубчатых механизмов используют зацепление Новикова, в котором профиль зуба выполнен по окружности.

Окружности, которые катятся в зацеплении без скольжения друг по другу, называются начальными (D).

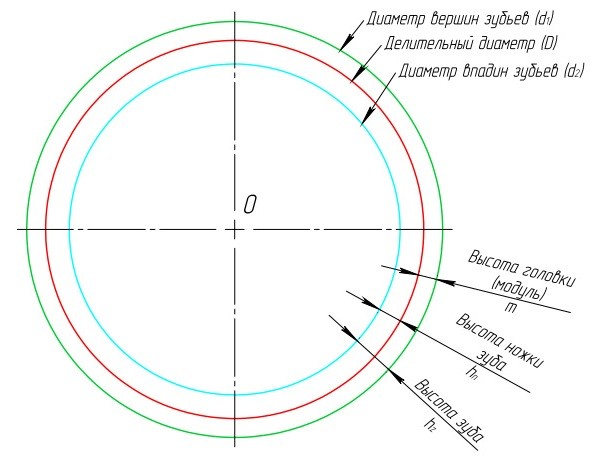
Окружности, огибающие головки зубьев зубчатых колёс, называются окружностями головок (d₁).

Окружности, огибающие ножки зубьев зубчатых колёс, называются окружностями ножек (d₂).

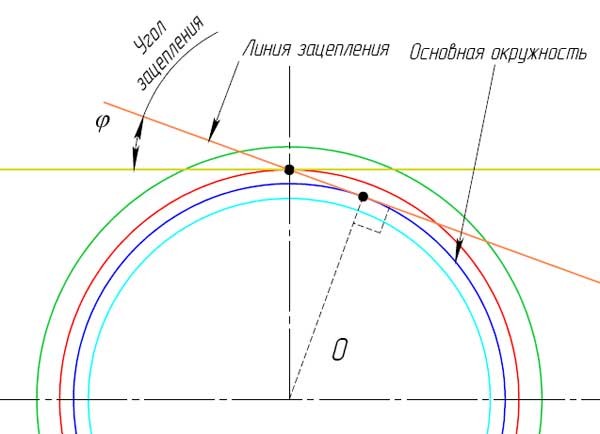
Окружности, по которым катятся прямые, образующие эвольвенты зубьев первого и второго колёс, называются основными окружностями.

Окружность, которая делит зуб на головку и ножку, называется делительной окружностью (D).

Для нулевых (некорригированных) колёс начальная и делительная окружности совпадают.

Расстояние между одноимёнными точками двух соседних профилей зубьев зубчатого колеса называется шагом по соответствующей окружности.

Шаг можно определить по любой из пяти окружностей. Чаще всего используют делительный шаг p =2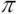r/z, где z – число зубьев зубчатого колеса. Чтобы уйти от иррациональности в расчётах параметров зубчатых колёс, в рассмотрение вводят модуль, измеряемый в миллиметрах, равный

Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности (D) к числу зубьев z или отношению шага p к числу «пи» .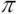

Модуль зубчатого колеса стандартизованы, что является основой для стандартизации других параметров зубчатых колёс.

Основные формулы для расчета эвольвентного зацепления:

Делительный диаметр рассчитывается по формуле:

Диаметр вершин зубьев рассчитывается по формуле:

d₁=D+2m

Диаметр впадин зубьев рассчитывается по формуле:

d₂=D-2*(c+m)

где с — радиальный зазор пары исходных контуров. Он определяется по формуле:

с = 0,25m

Диаметр основной окружности, развертка которой и будет составлять эвольвенту, определяется по формуле:

От автора. Я нашел в интернете полезную программку в Excel 2007. Это автоматизированная табличка для расчета всех параметров прямозубого зубчатого колеса.

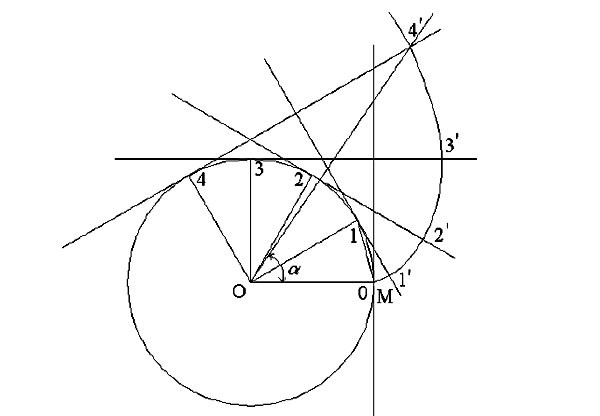
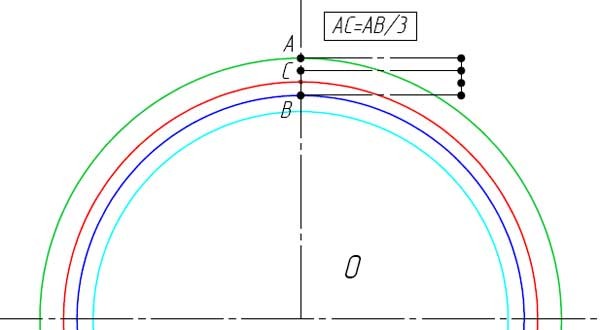
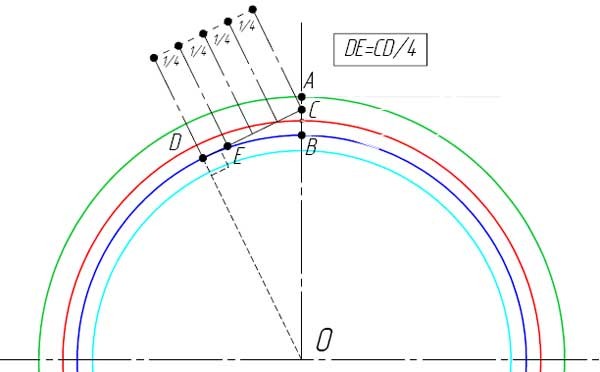
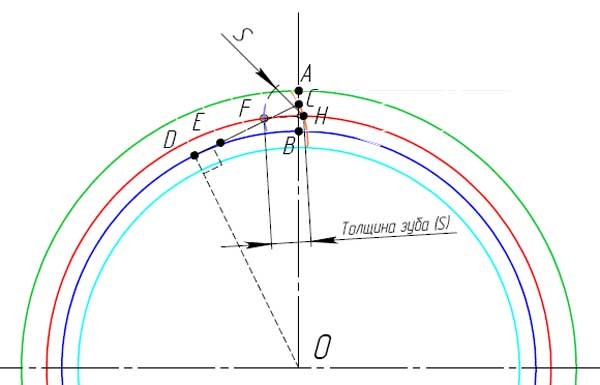
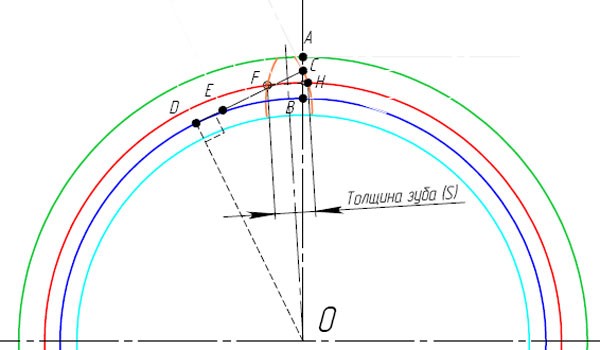
Итак, приступим к графическому построению профиля зубчатого колеса.

Вот и готов профиль зуба прямозубого зубчатого колеса. В этом примере использовались следующие параметры:

На этом первая часть урока является завершенной. Во второй части (видео) мы рассмотрим как применить полученный профиль зуба для построения модели зубчатого колеса. Для полного ознакомления с данной темой («зубчатые колеса и зубчатые зацепления», а также «динамические сопряжения в SolidWorks») необходимо вместе с изучением этого урока изучать урок №24.

Еще скажу пару слов о специальной программе, производящей расчет зубчатых колес и генерацию модели зубчатого колеса для SolidWorks. Это программа Camnetics GearTrax.

P.S.(16.03.2010) Скачать Camnetics GearTrax

А теперь переходим с следующей части урока.

Толщина зуба по дуге делительной
окружности

s = Пи*m/2 = 1.57 m = 1.57 * 5 = 7.85

Я предыдущие удалю, чтобы не путать людей.

Даже колеса в библиотеке SolidWorks прорисованы упрощенно. При изготовлении
зубчатых колес (если Вы знаете) используется зуборезной инструмент (долбежка,
фрезеровка, шлифовка). Этот инструмент уже профилирован, тем более зубчатые шестерни
стандартизированы.

Высота головки нормальных зубчатых колес равна модулю.

Источник