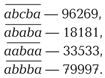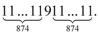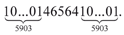Что такое числа палиндромы

Палиндромами так же являются квадраты таких чисел, как 11, 111, 1111 и т д. А именно:

11112 = 1 234 321 и т. д.
Интересно! что
1 + 2 + 1 = 4 = 2(во 2степени)

1 + 2 + 3 + 2 + 1 = 9 = 3(во 2степени)

1 + 2 + 3 + 4 + 3 + 2 + 1 = 16 = 4(во 2степени)

1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25 = 5(во 2степени)
Каждое из подобных чисел, можно изложить в виде неправильных дробей:
121=22х22/1+2+1
12321 =333х333/1+2+3+2+1
1234321=4444х4444/1+2+3+4+3+2+1
и так далее.

Наконец, для деления получаем:
82:41=28:14
62:31=26:13
— произведение первой цифры числа N1 на вторую цифру числа N2 равно произведению двух других их цифр: х1.у 2 = х2.у 1 (вы заметили связь между примерами на деление и умножение?).
https://www.nkj.ru/archive/articles/10656/

Особенно наглядно свойственное палиндрому «вечное движение» (вращение) проявляется в циклических палиндромах, или круговертнях, то есть в текстах, одинаково читаемых в обе стороны, но уже при записи вдоль окружности:

Еще одной разновидностью палиндрома является монопалиндром (термин А. Бубнова), т. е. единый палиндромный текст, записанный в несколько строк:

1. ортогонал: друг // враг (С. Ф.)
(Иллюстрация 2)
2. опрокидень: Звезда // звезда (Д. Авалиани)
(Иллюстрация 3)
3. опрокидень: Ты Бог // гад ты (С. Ф.)
(Иллюстрация 4)
В свою очередь наиболее перспективным из этих двух подвидов поворотня представляется опрокидень. Во всяком случае, примеров опрокидней известно на порядок больше, нежели ортогоналов. Поэтому заострим свое внимание именно на них.
Уже из приведенных выше примеров становятся видны принципиальные отличия опрокидня от палиндрома.
Во-первых, палиндромные строчки объективны и практически не зависят от индивидуальности автора. Поэтому-то так часты пересечения у любителей палиндромов. Опрокидни же сугубо индивидуальны, интимны, целиком зависят от почерка и фантазии автора:
1. Совсем я плох // хочу в народ.
(Иллюстрация 5)
2. Нимфа // вернись
(Иллюстрация 6)
3. Вернись // никогда (Д. Авалиани).
https://www.nkj.ru/archive/articles/10480/

Простейшие слова-палиндромы: мим, дед, наган, заказ, кабак, казак, мадам, шалаш. Самое длинное слово-палиндром, существительное, содержит 7 букв — ротатор. А если не требовать именительного падежа и единственного числа, то рекордсменом будет слово манекенам.

Будущие, ищу дуб,
Но сила ли сон?

* * *
Иль обида ради боли?

Доктор геолого-минералогических наук, кандидат физико-математических наук Б. ГОРОБЕЦ отмечает, что в русских палиндромах неизменно нечетное количество букв
https://www.nkj.ru/archive/articles/538/
Первый неожиданный результат был получен при частотном анализе распределения слов по числу букв. Почти все слова-палиндромы русского языка насчитывают нечетное число букв, от 1 до 11 (синие линии на гистограмме). Ничего подобного нет среди обычных, то есть несимметричных, слов (красные линии на гистограмме, демонстрирующие частотность слов, взятой из Частотного словаря русского языка, 1977, с.930). Гистограммы различаются настолько разительно, что нет смысла приводить математические выкладки по проверке статистической гипотезы о значимости указанного различия. Хотя сделать это несложно, и можно показать, что риск ошибки в сделанном выводе не превышает 0,01%.

Итак, «закон нечетности» распространяется исключительно на буквенно-симметричные словоформы, то есть на палиндромы! Однако, разумеется, это утверждение требует более строгой математико-лингвистической проверки путем подсчета слов со сдвоенным центром, имеющих как четное, так и нечетное число букв.

Замечательно, что действие «закона нечетности» распространяется не только на слова, но и на палиндромные фразы и более сложные тексты. Случайная выборка из 114 фраз у 33 авторов показала, что их доля с четным числом букв составляет 12,3%. У классика жанра Д. Авалиани она равна 13,5% в выборке из 200 фраз. Отсюда средняя доля центро-симметричных фраз, то есть фраз с центральной буквой, близка к 88% (тоже, кстати, цифровой палиндром!).

Естественен вопрос: а для чего все это нужно? Законы словообразования (если они действительно законы, выраженные количественно) действуют специфично и объективно на данное множество элементов, помогают формировать ту научную базу данных, которая необходима для создания и совершенствования новых информационных технологий, в частности кодирования и декодирования сообщений, переводов, распознавания образов (слов, слогов) в сигнале на фоне шума. И здесь нужны сведения о частотности слов в речи и литературе различных стилей. Эту работу еще предстоит выполнить.

Амфирифма
Сологолос
(В. Рыбинский)

Анархоохрана
Микрозорким
Маревоверам
Суперэпус
Синепенис
Трах-арт
Тревыверт
(В. Гершуни)

Лохохохол
(Джети
Автоботва
Аквалавка
Пракарп
Ретропортер
(Б. Гринберг)

Оленинело
(Ю. Телесин)

Девовед
Монгологном
Мордодром
(В. Хромов)

Икотопотоки
(Л. Адрианов)

Артсестра
Иноони
(Г. Лукомников)

Коненок
(К. Соприцкий)

Киторотик
(П. Нагорских)

Речевечер
(С. Красовицкий)

МакроЛоркам
МикроГорьким
Сотанатос
Солововолос
(С. Федин)

Тревоговерт
(Д. Минский)

Китокотик
Лифонофил (лифон жарг.- лифчик)
Недороден
Ротомотор
(Б. Горобец)

Конещенок
Недеееден
(Б. Гольдштейн)

Источник

Палиндромы и «перевёртыши» среди простых чисел

Числовой палиндром — это натуральное число, которое читается слева направо и справа налево одинаково. Иначе говоря, отличается симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным. Палиндромы встречаются в некоторых множествах чисел, удостоенных собственных названий: среди чисел Фибоначчи — 8, 55 (6-й и 10-й члены одноимённой последовательности); фигурных чисел — 676, 1001 (квадратное и пятиугольное соответственно); чисел Смита — 45454, 983389. Указанным свойством обладает также всякий репдиджит, например 2222222 и, в частности, репьюнит*.

Палиндром можно получить как результат операций над другими числами. Так, в книге «Есть идея!» известного популяризатора науки Мартина Гарднера в связи с этой задачей упоминается «гипотеза о палиндромах». Возьмём любое натуральное число и сложим его с обращённым числом, то есть записанным теми же цифрами, но в обратном порядке. Проделаем то же действие с получившейся суммой и будем повторять его до тех пор, пока не образуется палиндром. Иногда достаточно сделать всего один шаг (например, 312 + 213 = 525), но, как правило, требуется не менее двух. Скажем, число 96 порождает палиндром 4884 только на четвёртом шаге. В самом деле:

А суть гипотезы в том, что, взяв любое число, после конечного числа действий мы обязательно получим палиндром.

Можно рассматривать не только сложение, но и другие операции, включая возведение в степень и извлечение корней. Вот несколько примеров того, как при их помощи из одних палиндромов получаются другие:

До сих пор мы рассматривали в основном составные числа. Теперь обратимся к числам простым. В их бесконечном множестве имеются немало любопытных экземпляров и даже целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причём двадцать приходятся на первую тысячу, из них четыре числа однозначные — 2, 3, 5, 7 и всего одно двузначное — 11. С такими числами связано немало интересных фактов и красивых закономерностей.

Во-первых, существует единственный простой палиндром с чётным числом цифр — 11. Другими словами, произвольный палиндром с чётным числом цифр, бóльшим двух, число составное, что нетрудно доказать на основе признака делимости на 11.

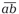
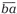
Во-вторых, первой и последней цифрами любого простого палиндрома могут быть только 1, 3, 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Любопытно, что все простые двузначные числа, записанные с помощью перечисленных цифр (за исключением 19), можно разбить на пары чисел-«перевёртышей» (взаимно обращённых чисел) вида и , где цифры a и b различны. Каждая из них, независимо от того, какое число стоит на первом месте, читается одинаково слева направо и справа налево:

Заглянув в таблицу простых чисел, мы обнаружим аналогичные пары, в записи которых присутствуют и другие цифры, в частности, среди трёхзначных чисел подобных пар наберётся четырнадцать.

Кроме того, среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1:

Аналогичная картина наблюдается и у бо`льших простых чисел, например:

Простые числа-палиндромы могут «задаваться» разными симметричными формулами, которые отражают особенности их записи. Это хорошо видно на примере пятизначных чисел:

Кстати, простые многозначные числа вида 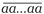встречаются, очевидно, только среди репьюнитов. Таких чисел известно пять. Примечательно, что у каждого из них количество цифр выражается простым числом: 2, 19, 23, 317, 1031. А вот среди простых чисел, у которых все цифры, кроме центральной, единицы, был обнаружен палиндром весьма внушительной длины — в нём 1749 цифр:

Вообще среди простых чисел-палиндромов встречаются удивительные экземпляры. Вот лишь один пример — числовой гигант

А интересен он тем, что содержит 11 811 цифр, которые можно разбить на три палидромические группы, причём в каждой группе количество цифр выражается простым числом (5903 или 5).

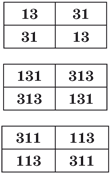
Любопытные палиндромические закономерности просматриваются и в группах простых чисел, в записи которых присутствуют определённые цифры. Скажем, только цифры 1 и 3, причём в каждом числе. Так, двузначные простые числа составляют упорядоченные пары 13 — 31 и 31 — 13, из шести трёхзначных простые сразу пять чисел, среди которых есть два палиндрома: 131 и 313, а ещё два числа образуют пары «перевёртышей» 311 — 113 и 113 — 311. Во всех этих случаях составленные пары наглядно представляются в виде числовых квадратов (рис. 1).

Своими свойствами они напоминают магический и латинский квадраты. Например, у среднего квадрата сумма чисел, стоящих в каждой строке и в каждом столбце, равна 444, на диагоналях — 262 и 626. Сложив числа из всех клеток, получим 888. И что характерно, каждая сумма — палиндром. Даже просто выписывая без пробела несколько чисел из одной таблицы, получим новые палиндромы: 3113, 131313131 и т. д. Какое наибольшее число можно составить таким способом? Будет ли оно палиндромом?

Если в каждую из пар 311 — 113 и 113 — 311 добавить 131 или 313, образуются четыре палиндромические тройки. Запишем одну из них в столбик:

Как видим, и сами числа, и нужная их комбинация дают о себе знать при прочтении в разных направлениях. Кроме того, расположение цифр симметрично, а их сумма в каждой строке, каждом столбце и на одной из диагоналей выражается простым числом − 5.

Надо сказать, рассмотренные числа интересны и сами по себе. Например, палиндром 131 — простое циклическое число: при любых последовательных перестановках первой цифры на последнее место он порождает простые числа 311 и 113. Можете ли вы указать другие простые палиндромы, обладающие таким же свойством?

А вот пары чисел-«перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр оказались связаны хитрым образом:

(1 + 1 + 3) 2 = 1 + 2 + 7 + 6 + 9.

Добавим, что среди натуральных чисел имеются и другие пары «перевёртышей» с подобным свойством: 103 — 301, 1102 — 2011, 11113 — 31111 и др. Чем объясняется подмеченная закономерность? Чтобы ответить на этот вопрос, нужно понять, что особенного в записи указанных чисел, какие цифры и в каком количестве могут в ней присутствовать.

Из простых чисел-палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.

Вот, например, красивая комбинация из простых палиндромов, записанных с помощью 1 и 3 (кроме первого, рис. 2). Особенность этого числового треугольника в том, что один и тот же фрагмент повторяется трижды, не нарушая симметрию рисунка.

Легко видеть, что общее количество строк и столбцов — число простое (17). К тому же простые числа и суммы цифр: выделенных красным фрагментов (17); каждой строки, за исключением первой (5, 11, 17, 19, 23); третьего, пятого, седьмого и девятого столбцов (7, 11) и «лесенки» из единиц, образующей боковые стороны треугольника (11). Наконец, если двигаться параллельно указанным «сторонам» и складывать по отдельности цифры третьего и пятого рядов (рис. 3), получим ещё два простых числа (17, 5).

Продолжая построение, можно сконструировать на основе данного треугольника более сложные фигуры. Так, ещё один треугольник с аналогичными свойствами нетрудно получить, двигаясь с конца, то есть начать с последнего числа, вычёркивая на каждом шаге две одинаковые симметрично расположенные цифры и переставляя или заменяя другие — 3 на 1 и наоборот. При этом сами цифры следует выбирать с таким расчётом, чтобы образующееся в итоге число оказалось простым. Объединив обе фигуры, получим ромб с характерным узором из цифр, скрывающим в себе немало простых чисел (рис. 4). В частности, сумма выделенных красным цветом цифр равна 37.

Другой пример — треугольник, полученный из исходного после добавления к нему шести простых палиндромов (рис. 5). Фигура сразу привлекает внимание своим изящным обрамлением из единиц. Её окаймляют два простых репьюнита одинаковой длины: 23 единицы составляют «основание» и ещё столько же — «боковые стороны» треугольника.

Ещё несколько фигур

Можно составить также многоугольные фигуры из чисел, обладающие определёнными свойствами. Пусть требуется построить фигуру из простых палиндромов, записанных с помощью 1 и 3, у каждого из которых крайние цифры — единицы, а сумма всех цифр и общее количество единиц в строке — простые числа (исключение — однозначный палиндром). Кроме того, простым числом должно выражаться общее количество строк, а также цифр 1 либо 3, встречающихся в записи.

На рис. 6 приведено одно из решений задачи — «домик», сконструированный из 11 различных палиндромов.

Конечно, не обязательно ограничиваться двумя цифрами и требовать наличия в записи каждого используемого числа всех указанных цифр. Скорее, наоборот: ведь именно их необычные сочетания придают своеобразие узору фигуры. В подтверждение этому приведём несколько примеров красивых палиндромических зависимостей (рис. 7−9).

Теперь, вооружившись таблицей простых чисел, вы и сами сконструируете фигуры вроде предложенных нами.

А напоследок ещё одна диковинка — треугольник, буквально пронизанный вдоль и поперёк палиндромами (рис. 10). В нём 11 строк из простых чисел, а столбцы образованы репдиджитами. И главное: ограничивающий фигуру с боков палиндром 193111111323111111391 — число простое!

Комментарии к статье

*Число Смита — составное число, сумма цифр которого равна сумме цифр его простых делителей.

Репдиджит — натуральное число, в записи которого все цифры одинаковые.

Репьюнит — натуральное число, записанное с помощью одних только единиц.

Источник

Что такое числа палиндромы

Назовем исходное число и число с переставленными в обратном порядке цифрами взаимно обратными.

Выяснено, что сложение некоторых взаимно обратных чисел приводит к образованию числа-палиндрома. Но для многих взаимно обратных чисел такое число палиндром при сложении не образуется. А что будет, если в этом случае сложить результат сложения с его взаимно обратным числом?

Задание:

Как зависит результат сложения от суммы цифр исходного числа?

Ответ можешь посмотреть здесь.

Примерами являются все однозначные числа, двузначные вида αα, такие как 11 и 99, трехзначные числа вида αβα, например 535 и так далее.

Слово палиндром произошло от греческого слова palindromos ( palнndromos ) , обозначающего “вновь бегущий назад”. Палиндромами могут быть не только числа, но также и слова, предложения и даже тексты. Примером может служить слова ротор, радар или известная фраза “А роза упала на лапу Азора”, которые читаются одинаково как слева направо, так и справа налево. В английском языке это слова «Radar», «I», «Eve», «Deed, «Redivider» и фразы «Madam, I’m Adam, «A man, a plan, a canal. Panama «. Примеры палиндромов встречаются и в природе – молекула ДНК, например, имеющая комплиментарные основания. В ДНК есть отрезки, имеющие одинаковую нуклеотидную последовательность при чтении по обеим цепям спирали в одинаковом направлении. Общее число таких «перевертышей» в геноме человека оценено от 100 тыс. до 1 млн. При этом они относительно равномерно распределены по ДНК.

Греческие поэты еще в 300 году до н.э. начали употреблять палиндромы.

Источник

Проект «Удивительные числа палиндромы»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

МКОУ Первотроицкая средняя школа

«Удивительные числа палиндромы»

Выполнила: ученица 9 класса

Пилипейко Олеся Ивановна,

Формула и примеры палиндромов………………………………………………………..…10-11

Список использованной литературы и интернет- ресурсов………. 14

У каждого ученика есть любимые предметы в школе. Мне больше всего нравятся уроки математики. И как-то я услышала о таком математическом понятие, как палиндром. Сначала было непонятно, что это такое? Но когда я стала интересоваться этой темой, то оказалось очень интересно и занимательно. Я люблю узнавать что-то новое. Мне информация стала интересной, и я решила изучить её.

Палиндро́м (от греч. πάλιν — «назад, снова» и греч. δρóμος — «бег») — число (например, 404), буквосочетание, слово (например, топот) или текст, одинаково (или почти одинаково) читающиеся в обоих направлениях.

Математические палиндромы обладают тем же свойством, т.е. число отличается симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным.

Предмет исследования – множество простых чисел.

Объект исследования – числа палиндромы.

Цель моей проектной работы : рассказать о «магических» свойствах палиндромов, самой узнать о них много нового и попытаться составить свои математические палиндромы.

1) Изучить теоретический материал по данной теме;

2) Научиться составлять палиндромы в различных дисциплинах;

3) Расширить кругозор;

4) Показать применение математики в различных областях.

5) Провести опрос среди учащихся 8-9 классов.

Гипотеза: Нас окружают иногда очень интересные слова и числа, но мы редко задумываемся об их происхождении и предназначении. Мир сложно прекрасен и загадочно прост.

Отдельные палиндромические словосочетания и фразы известны с глубокой древности, когда им зачастую придавался магически-сакральный смысл. Например, фраза: «На в лоб, болван», использовавшаяся русскими скоморохами.

Из глубины веков до нас дошли не только латинские, но и греческие

палиндромы. В «Поэтическом словаре» А.Квятковского сказано: «В византийском храме Софии в Константинопо­ ле на мраморной купели было вырезано следующее палиндром ное изречение: « nisponanomimatamimonanopsin », означающее: «Омывайте не только лицо, но и ваши грехи».

Уже к Х-Х I вв. палиндромы распространились сначала в Ита­ лии, а затем и в

Авторское творчество в области палиндрома начинается, по-видимому, в Средние века. Особенно всё волшебство палиндромов ощущали в древности, когда палиндромные фразы казались магическими. Самый древний из известных палиндромов был написан в IV в.: «SATOR AREPO TENET OPERA ROTAS» («Сеятель Арепо с трудом держит колеса»). Впрочем, зачем упорный сеятель держал колеса, не имело никакого значения для тех, кто рисовал этот палиндром на стенах домов. Главное было то, что из него можно было составить дивную вещицу – так называемый магический квадрат, где выражение могло читаться как вертикально, так и горизонтально, как слева направо сверху вниз, так и наоборот:

Из-за удивительных свойств этот палиндром считался оберегом от болезней и злых духов. Чтение наоборот в целом и палиндромы в частности имели огромное значение в магических ритуалах самых разных культур и всегда считалось так или иначе связанным со злом. Палиндромальные руннетейны (сочетания рун, рунические «фразы»), одинаково читающиеся с любого конца или по кругу, считались наиболее могущественными; многие сакральные рунические слова были палиндромами.

Определенную магию приписывали и математическим палиндромам из-за их необыкновенных свойств. Еще с древности люди заметили такие необъяснимые закономерности чисел-перевертышей, и эта загадка сохранилась и до наших времен.

Вы, наверное, все помните книгу о приключениях Буратино. Помните, как строгая Мальвина учила Буратино писать? Она велела написать такую фразу: “А роза упала на лапу Азора” и велела прочитать “наоборот”. Эта фраза читается слева направо и справа налево. Это фраза-палиндром (в переводе — перевертыш). Слова: ШАЛАШ, РАДАР, ТОПОТ, КОК, КАЗАК — тоже палиндромы.

Числовые палиндромы – это натуральные числа, которые одинаково читаются справа налево и слева направо. Иначе говоря, отличаются симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным.

Например: 121; 676; 1331; 4884; 94949; 1177711; 1178711 и т. д.

Изучая палиндромы, я задалась вопросом: «Как из других чисел можно получить палиндромы?»

Палиндром можно получить как результат операций над другими числами. Для этого воспользуемся известным алгоритмом.

Алгоритм получения палиндрома

Возьми любое двузначное число

Переверни его (переставь цифры справа налево)

Переверни полученное число

Повторяй аналогичные действия до тех пор, пока не получится палиндром

Источник

Откладываем палиндромы на новый год

Это короткая статья о том, как я занялся задачей об отложенных палиндромах в 2020-ом году и установил мировой рекорд уже в 2021-ом. Суть задачи предельна проста: найти такое число, простые преобразования которого позволяют получить палиндром. Тем не менее, уже больше 20-и лет эта проблема не имеет строгого решения.

Моё знакомство с отложенными палиндромами началось в ночь с 10 на 11 декабря на просторах ютуба. Я обдумывал квадрат Паркера и перебирал видео из поисковой выдачи. На фоне вполне привычных переводов от Mad Astronomer выделялся репортаж телеканала Мир-24 о московском школьнике-рекордсмене

Меня привлекла как сама задача, так и россыпь негативных комментариев под видео, поэтому я отложил ролик на утро: чтобы разобраться в сути открытия. В следующем пункте я попытаюсь ввести читателя в курс дела.

Проблема 196 и отложенные десятичные палиндромы

Палиндром — это объект, который может быть представлен в виде упорядоченного набора символов (слово, строка, число) и обладает свойством симметрии относительно своего центрального элемента (или пары таких совпадающих центральных элементов, если палиндром состоит из четного числа символов). Проще говоря, мы называем палиндромом то, что одинаково читается слева направо и справа налево. Например, слово «довод» является палиндромом из русских букв, а число 1991 — палиндромом из цифр.

В конце XX века математик и программист Ван Лэндингхэм придумал простой алгоритм, который с высокой вероятностью может превратить случайное натуральное число в палиндром.

Число 12000700000025339936491 является отложенным палиндромом глубины 288

Это число содержит 23 знака, а соответствующий ему точный палиндром — 142 знака, поэтому его сложно найти полным перебором всех начальных для алгоритма Лэндингхэма значений. Но изучение некоторых важных свойств отложенных палиндромов помогает оптимизировать поиск, вычеркнув целые классы как повторяющихся, так и гарантированно «слабых» относительно текущего рекорда значений.

О псевдорекордах и критериях принятия решений

Рассмотрим первые несколько ступеней вывода палиндрома из 288-ишагового рекорда:

Важно обратить внимание на то, что цифры 5 в начале и конце суммы 53028297704050680282925, полученной после двух шагов операции «перевернуть и сложить», являются суммами крайних элементов 3 и 2 числа 31464693352025340636512 в «прямой» записи и соответствующих им крайних элементов 2 и 3 в обратной записи того же числа:

Так случается потому что при сложении «в столбик» числа и его обратной записи, друг под другом оказываются первая и последняя цифра одного и того же числа, вторая и предпоследняя и так далее. При этом сложение можно выполнять не только школьным методом справа налево, но и более сложным — слева направо — также без искажения результата. При сложении справа налево мы добавляем лишнюю единицу к следующему разряду, если в предыдущем сумма была 10 или больше. При сложении же слева направо мы наоборот вычитаем десятку из предыдущего разряда каждый раз, когда в текущем разряде значение суммы на единицу меньше того, которое мы ожидаем исходя из свойств возвратности/симметричности результата. В общем же случае, сложение слева направо выполняется с постоянной коррекцией уже вычисленных разрядов на единицу переноса. Изучив этот процесс, можно строго доказать, что в любой последовательности чисел такой, что каждое следующее является результатом операции «перевернуть и сложить» над предыдущим, все числа кроме первого гарантированно являются 0-возвратными или 1-возвратными.

Возвратность — это некое условное обозначение для чисел, которые близки к палиндромам, но не являются ими. Так, 0-возвратное число имеет вид:

То есть при прочтении справа налево каждая цифра может либо совпадать с цифрой исходного (записанного слева направо) числа в том же разряде, либо отличаться от нее не более чем на единицу (следуют из правил сложения и того факта, что сумма двух цифр никогда не превышает 18-и без учета единицы переноса и 19-и с учетом переноса). Рассмотрим вывод числа 12000700000025339936491 и заметим, что большинство промежуточных значений 0-возвратны. Так в числе 21563604352025339646413 крайние разряды 2 и 3 отличаются на единицу, второй и предпоследний совпадают и равны 1, третий сначала и с конца равны соответственно 5 и 4 и отличаются на единицу и так далее.

Некоторые промежуточные значения вывода палиндрома не являются 0-возвратными, но из них можно сделать 0-возвратное удалением первой цифры. Так происходит когда складываются прямая и обратная запись числа, крайние цифры которого либо в сумме превышают 9, либо равны 9 и при сложении получают дополнительную единицу из-за переноса второго слева разряда. Таким является, например, число: 105956506309091459564960. Действительно: , , , и т.д.
Свойство возвратности позволяет описывать огромные семейства чисел, которые после одной или нескольких операций «перевернуть и сложить» приходят к одному и тому же числу. Так, рассмотрим рекорд, установленный московским школьником в 2017-ом году:

Число 1999291987030606810 является отложенным палиндромом глубины 261

Зная, что симметричное изменение разрядов (увеличение первого и уменьшение второго на одно и то же число, увеличение/уменьшение второго одновременно с уменьшением/увеличением предпоследнего и так далее) может сохранять результат операции «перевернуть и сложить» над исходным числом, выполним следующие шаги:

Если бы мы взяли число 1920000192, то оно также оказалось бы отложенным на 4 шага палиндромом, но уже с результатом 69960006996. Этот способ работает с любым
отложенным палиндромом при достаточно большом количестве нулей — разделителей. Если нулей будет недостаточно, то на определенном этапе результат сложения в правой половине числа начнет влиять на сумму слева и вывод изменится. Например, число 192192 на третьей итерации алгоритма даст число 1636635, где результат 1635 справа превратился в 635, а 1635 слева превратились в 1636 из-за «наезда» поразрядных сумм друг на друга.

Используя это свойство, можно легко побить как «рекорд» Щебетова, предложив число 1999291987030606810000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001999291987030606810, отложенное на 261 шаг, так и действующий рекорд Нобелена, заменив его числом 120007000000253399364910000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000012000700000025339936491, отложенным на 288 шагов.

При этом сама задача вывода отложенного палиндрома глубины большей чем n при наличии сколь угодно большой базы отложенных палиндромов глубины n, является вычислительно тяжелой, поэтому предлагаю:

Метод неопределенного перебора

Такая простая в бытовом понимании операция как «перевернуть и сложить» уже представляет собой большую проблему для теоретического анализа. Трудно представить, что операция «обратного вывода», результатом которой является (необязательно непустое) множество всех 0- и 1-возвратных чисел, приводящих к исходному числу после фиксированного количества k итераций алгоритма Лэндингхэма, может быть строго алгоритмизирована и даже описана теоретически.

Рассмотрим пример. Число 1137301 является отложенным палиндромом глубины 15 — полный вывод здесь. Попробуем получить из него отложенный палиндром глубины 16:

Для 7-изначного числа 1137301 результат операции одношагового вывода может содержать как 0-возвратные 7-изначные числа (левая половина дерева вывода), так 1-возвратные 6-изначные решения (правая половина изображения). Рассмотрим левую половину:

Метод неопределенного перебора находит те же решения, что и описанная выше модификация метода неопределенных коэффициентов, но является одновременно менее логичным для человека и более удобным для программной реализации. Его суть можно описать четырьмя простыми этапами, на которые разбиваются все итерации обратного вывода:

Частичная реализация метода неопределенного перебора на примере процедуры R21:

После полной реализации набора вспомогательных процедур, я взял в качестве начального значение 105956506309091459564960, так как оно отстоит от текущего рекорда на 3 шага (отложено на 285 шагов против 288 в рекорде), но при этом может является суммой только 23-хзначного числа и его обратной записи. Так мы сочетаем сравнительно небольшие размер кода и продолжительность вычислений с достаточно объемным множеством обратно выводимых значений (отложенных палиндромов глубины 286 и более, проходящих через число 105956506309091459564960). На случай, если рекорд не будет найден на этом этапе, программа продолжает работу, беря другое — более «тяжелое» по времени расчета — начальное значение, что видно на скриншоте.

Результат работы моей программы:

Использование в нашей реализации метода неопределенного перебора процедур R21, R22 и R23, восстанавливающих 21-23-хзначные 0-возвратные и 22-24-хзначные 1-возвратные значения, гарантирует, что из числа 105956506309091459564960 невыводим ни один отложенный на 290 и более шагов палиндром. Более того, все 289-ишаговые решения, проходящие через число 105956506309091459564960, оказываются непосредственно выводимы из числа 16937872231012117762051 при помощи 0-возвратной ветки процедуры R23 — вывод 0-возвратного 23-хзначного числа из другого 0-возвратного 23-хзначного.

Послесловие

Теория чисел долгое время не считалась полноценной математической дисциплиной, поэтому сегодня математики легко справляются со сложнейшими задачами дифференциальной алгебры, топологий, но практически беспомощны перед проблемами элементарных свойств десятичных чисел. Математический анализ позволяет эффективно искать числа, критерий проверки для которых задан функционально. Но операция «перевернуть и сложить» в десятичной системе исчисления из-за объективных причин, таких как перенос единицы при превышении десятка в поразрядной сумме, не может быть описана функционально.

Занимаясь поиском отложенных палиндромов, необходимо уделять больше внимания разработке новых методов вывода и проверки решений, а не численным рекордам как таковым. В моей работе были предложены не только наибольшие из известных сегодня решений, но и новый алгоритм для работы с «отложением» как со строгой математической операцией. Так я вношу свой скромный вклад в методологию решения численных задач в целом.

Источник