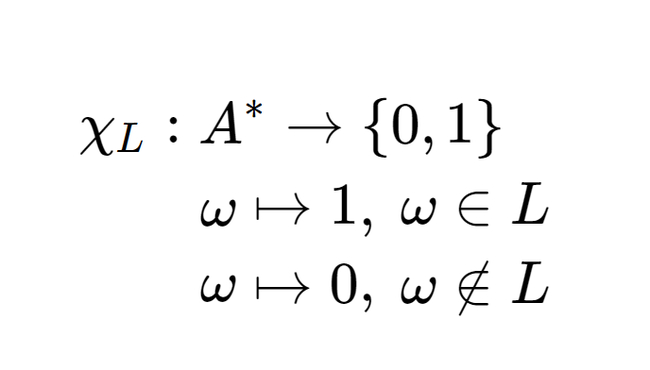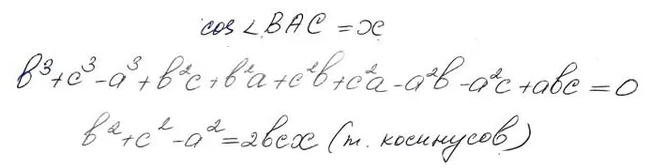Что такое четырехмерное пространство простыми словами
Как легко понять четырехмерное пространство (17 фото)
Из моего опыта вживую, надо начать с 2-х мерного пространства, подготовить мозг. Поэтому берем несчастных 2-мерных существ, живущих в 2-мерном мире, на плоскости. В Плоском мире )) Как им понять наш трехмерный мир? А очень просто.
Вот это — квадрат, фигура, хорошо знакомая плоскостникам.
А вот фигура, несколько странная и непонятная плоскостникам
Мы с вами, жители трехмерного мира, легко узнаем в ней куб, составленный из квадратов. Хотя бы еще не выходили из плоскости, но мы, трехмерники, ясно понимаем: куб, че тут еще думать )))
Однако жители двумерного мира, не умеющие мыслить как мы, тремя измерениями, видят в ней другие фигуры, с их точки зрения:
Из коих только 1 и 2 — квадраты, а остальные — нечто перекошенное. С некоторой натяжкой плоскостники могут сказать, что фигуры 3, 4, 5 и 6 — это перекошенные квадратики. Вот это важный момент.
Это переход от двумерного мышления — к нашему трехмерному. Что вы видите на следующей картинке? Там разные фигуры — или все одни и те же, квадратики, просто в разных проекциях?
Мы, трехмерники, спокойно можем сказать, что это все — квадраты. И плоскостник, умеющий мыслить на одно измерение больше — может сказать то же самое. Что это проекции квадратов в его плоское измерение. Хотя все его двумерные сотоварищи будут видеть трапеции и только два квадрата.
Все, закончили с плоскостниками, возвращаемся в наше, трехмерное измерение.
Обычный куб я вам показывать не буду, покажу сразу: 4-х мерный куб )) Он еще носит название «тессеракт» или «гиперкуб». Это вот такая штука:
Чтобы легче его представить, вот он в других разных видах:
Представьте, что вы такое держите в руках. Я делал такие штуки из разных материалов, это не сложно
Что вы здесь видите? Кубик, к которому присоединены шесть призм? Ну, это если мы будем думать по нашему, по трехмерному. А если думать по четырехмерному, на одно измерение больше, то это 8 (восемь) кубов!
Восемь кубиков, соединенных гранями. Просто шесть из них искажены в призмы, так как наше пространство 3-мерное, а этот объект — 4-мерный. Тессеракт это 4-мерный куб. Гиперкуб. Все просто )))
Вернемся на секунду к плоскому миру, с меньшим числом измерений, чем у нас.
С точки зрения двумерников (у них всего 2 измерения), это разные фигуры. А с нашей трехмерной точки зрения ( 2+1 = 3 измерения) это все одна и та же фигура: квадрат, которую мы видим под разными углами.
И двухмерник тоже может понять, что это трехмерный квадрат, который он видит под разными углами. А вот это — трехмерный куб, который двумерник видит частично искаженным.
Ну вот и славненько. А если взять наше измерение, то становится понятно, что вот это — четырехмерный гиперкуб. Просто мы его видим частично искаженным.
Это восемь кубов, соединенных гранями. Сторонами. И если посмотреть на них с другой проекции, то можно увидеть КАЖДЫЙ куб. Просто нужно вращать тессеракт в 4-м измерении.
По счастью, народ наделал много гифок, в которых именно это и показывает. Что меняя 4-х мерную перспективу, можно видеть ВСЕ кубы. Но в нашем трехмерном мире — только по-очередно.
И квадраты тоже можно видеть все. Ведь куб состоит из квадратов, и тессеракт — тоже.
Наш, трехмерный куб — можно развернуть в двумерные квадраты.
И точно так же 4-х мерный тессеракт (он же гиперкуб) можно развернуть в наши 3-мерные кубы.
Стройте себе тессеракт на 3D принтерах, из спичек, зубочисток и пластилина, паяйте из проволоки, смотрите — и прорывайтесь в четвертое измерение!
Кстати. А существуют ли другие четырехмерные фигуры? Да. Вот это, например, 4-мерная равносторонняя гиперпирамида, если я не ошибаюсь.
Принципе тот же: взяли наши обычные пирамидки, исказили в 4-мерной проекции, соединили гранями.
Что такое четырехмерное пространство?
Представление мира в различных измерениях меняет то, как мы воспринимаем все вокруг, включая время и пространство. Думать о разнице между двумя измерениями и тремя измерениями легко, но что насчет четвертого? Важно понимать, что имеют в виду ученые и другие исследователи, когда говорят о различных измерениях: наш мир имеет три пространственных измерения: ширину, глубину и высоту, а четвертым измерением может быть время. Ученые много лет проводят исследования в попытках выяснить что же такое четвертое пространственное измерение, однако по причине того, что наблюдать четвертое измерение мы не можем, доказательства его существования найти очень трудно.
Моделирование движения камеры в четырёхмерном пространстве.
Сколько существует измерений?
Чтобы лучше понимать, на что может быть похоже четвертое измерение, давайте поближе посмотрим на то, что именно делает три измерения трехмерными, и, следуя этим идеям, подумаем о том, что такое четвертое измерение. Итак, длина, ширина и высота составляют три измерения наблюдаемого мира. Все три измерения мы можем наблюдать благодаря эмпирическим данным, а также органами чувств – такими как зрение и слух.
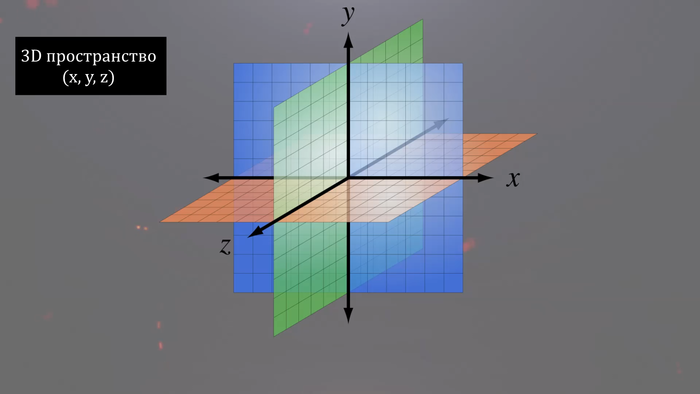
Определить положение точек и направления векторов в трехмерном пространстве можно вдоль опорной точки. Проще всего представить себе трехмерное пространство как трехмерный куб с тремя пространственными осями, которые определяют ширину, высоту и длину куба. Оси движутся вперед и назад, вверх и вниз, влево и вправо вместе со временем – измерением, которое мы непосредственно не наблюдаем, но воспринимаем. При сравнении 3D и 4D, учитывая наблюдения трехмерного пространственного мира, четырехмерный куб будет Тессерактом – объектом, который движется в трех измерениях, которые мы и воспринимаем и в четвертом, которое е можем наблюдать.
Четырехмерный куб (тессеракт) выглядит так
Еще больше статей о последних открытиях в области теоретической физики и высоких технологий читайте на нашем канале в Яндекс.Дзен. Там регулярно выходят статьи, которых нет на сайте.
Четырехмерные объекты и тени
Как пишет Sciencing.com, поскольку трехмерные существа отбрасывают тень на двумерную поверхность Куба, это привело исследователей к предположению о том, что четырехмерные объекты отбрасывают трехмерную тень. Вот почему можно наблюдать «тень» в трех пространственных измерениях, даже если непосредственно наблюдать четыре измерения нельзя.
Математик Генри Сегерман из университета штата Оклахома создал и описал свои собственные 4-мерные скульптуры. Точно так же, как трехмерный объект отбрасывает двумерную тень, Сегерман утверждал, что его скульптуры являются трехмерными тенями четвертого измерения. Хотя эти примеры теней не дают прямых способов наблюдения четвертого измерения, они являются хорошим индикатором того, как думать о четвертом измерении.
Фигуры математика Генри Сегермана выглядят так
Математики часто приводят аналогию с муравьем, идущим по листу бумаги, описывая границы восприятия относительно измерений. Муравей, идущий по поверхности бумаги, может воспринимать только два измерения, но это не значит, что третьего измерения не существует. Это просто означает, что муравей может непосредственно видеть только два измерения и выводить третье измерение через рассуждения об этих двух измерениях. Точно так же люди могут размышлять о природе четвертого измерения, не воспринимая его непосредственно.
Четырехмерный куб Тессеракт – это один из примеров того, как трехмерный мир, описываемый x, y и z, может расширяться в четвертый. Математики, физики и другие ученые могут представлять векторы в четвертом измерении, используя четырехмерный вектор, который включает в себя другие переменные, такие как w. Геометрия объектов в четвертом измерении более сложна, так как включает в себя 4-многогранники, которые являются четырехмерными фигурами. Эти объекты показывают разницу между 3D и 4D изображениями.
Существует ли жизнь в четвертом измерении?
То, как выглядели бы существа или жизнь в четырех измерениях, занимало ученых и других специалистов на протяжении десятилетий. В рассказе писателя Роберта Хайнлайна 1940 года «Дом который построил Тим» речь шла о постройке здания в форме Тессеракта. Писатель Клифф Пиковер представлял себе четырехмерных существ как «воздушные шары телесного цвета, постоянно меняющиеся в размерах. Эти существа будут казаться вам разрозненными кусками плоти, точно так же, как двумерный мир позволяет вам видеть только поперечные сечения и остатки мира трехмерного.»
Кадр из мультсериала «Футурама», 15 серия 7 сезона. Перед вами герои в 2D
Четырехмерная форма жизни может видеть вас изнутри точно так же, как трехмерное существо может видеть двумерное со всех сторон.
Однако точно ответить на вопрос о том, существуют ли 4D существа сегодня не может никто. Я полагаю, что даже концепция 4D-пространства ожесточенно обсуждается в физических лабораториях, хотя некоторые теории, такие как Теория струн и М-теория, используют существование нескольких измерений для объяснения нашей Вселенной. Важно также отметить, что биологически 4d жизнь не может существовать. А что вы думаете по этому поводу? Присоединятйесь к обсуждению этой темы в комментариях, а также с участниками нашего Telegram чата.
Что такое четырехмерное пространство?
Представление мира в различных измерениях меняет то, как мы воспринимаем все вокруг, включая время и пространство. Думать о разнице между двумя измерениями и тремя измерениями легко, но что насчет четвертого? Важно понимать, что имеют в виду ученые и другие исследователи, когда говорят о различных измерениях: наш мир имеет три пространственных измерения: ширину, глубину и высоту, а четвертым измерением может быть время. Ученые много лет проводят исследования в попытках выяснить что же такое четвертое пространственное измерение, однако по причине того, что наблюдать четвертое измерение мы не можем, доказательства его существования найти очень трудно.
Сколько существует измерений?
Чтобы лучше понимать, на что может быть похоже четвертое измерение, давайте поближе посмотрим на то, что именно делает три измерения трехмерными, и, следуя этим идеям, подумаем о том, что такое четвертое измерение. Итак, длина, ширина и высота составляют три измерения наблюдаемого мира. Все три измерения мы можем наблюдать благодаря эмпирическим данным, а также органами чувств – такими как зрение и слух.
Определить положение точек и направления векторов в трехмерном пространстве можно вдоль опорной точки. Проще всего представить себе трехмерное пространство как трехмерный куб с тремя пространственными осями, которые определяют ширину, высоту и длину куба. Оси движутся вперед и назад, вверх и вниз, влево и вправо вместе со временем – измерением, которое мы непосредственно не наблюдаем, но воспринимаем. При сравнении 3D и 4D, учитывая наблюдения трехмерного пространственного мира, четырехмерный куб будет Тессерактом – объектом, который движется в трех измерениях, которые мы и воспринимаем и в четвертом, которое е можем наблюдать.
Четырехмерные объекты и тени
Поскольку трехмерные существа отбрасывают тень на двумерную поверхность Куба, это привело исследователей к предположению о том, что четырехмерные объекты отбрасывают трехмерную тень. Вот почему можно наблюдать «тень» в трех пространственных измерениях, даже если непосредственно наблюдать четыре измерения нельзя.
Математик Генри Сегерман из университета штата Оклахома создал и описал свои собственные 4-мерные скульптуры. Точно так же, как трехмерный объект отбрасывает двумерную тень, Сегерман утверждал, что его скульптуры являются трехмерными тенями четвертого измерения. Хотя эти примеры теней не дают прямых способов наблюдения четвертого измерения, они являются хорошим индикатором того, как думать о четвертом измерении.
Математики часто приводят аналогию с муравьем, идущим по листу бумаги, описывая границы восприятия относительно измерений. Муравей, идущий по поверхности бумаги, может воспринимать только два измерения, но это не значит, что третьего измерения не существует. Это просто означает, что муравей может непосредственно видеть только два измерения и выводить третье измерение через рассуждения об этих двух измерениях. Точно так же люди могут размышлять о природе четвертого измерения, не воспринимая его непосредственно.
Четырехмерный куб Тессеракт – это один из примеров того, как трехмерный мир, описываемый x, y и z, может расширяться в четвертый. Математики, физики и другие ученые могут представлять векторы в четвертом измерении, используя четырехмерный вектор, который включает в себя другие переменные, такие как w. Геометрия объектов в четвертом измерении более сложна, так как включает в себя 4-многогранники, которые являются четырехмерными фигурами. Эти объекты показывают разницу между 3D и 4D изображениями.
Существует ли жизнь в четвертом измерении?
То, как выглядели бы существа или жизнь в четырех измерениях, занимало ученых и других специалистов на протяжении десятилетий. В рассказе писателя Роберта Хайнлайна 1940 года «Дом который построил Тим» речь шла о постройке здания в форме Тессеракта. Писатель Клифф Пиковер представлял себе четырехмерных существ как «воздушные шары телесного цвета, постоянно меняющиеся в размерах. Эти существа будут казаться вам разрозненными кусками плоти, точно так же, как двумерный мир позволяет вам видеть только поперечные сечения и остатки мира трехмерного.»
Четырехмерная форма жизни может видеть вас изнутри точно так же, как трехмерное существо может видеть двумерное со всех сторон.
Однако точно ответить на вопрос о том, существуют ли 4D существа сегодня не может никто. Я полагаю, что даже концепция 4D-пространства ожесточенно обсуждается в физических лабораториях, хотя некоторые теории, такие как Теория струн и М-теория, используют существование нескольких измерений для объяснения нашей Вселенной. Важно также отметить, что биологически 4d жизнь не может существовать.
Ничего не мешает существованию 4-го линейного измерения. И 5-го и 6-го и т.д. До бесконечности.
Дело в том, что окружающую нас вселенную мы воспринимаем с определённых позиций и с определёнными потребностями. И всё зависит от необходимости существовать (эффективно существовать) в этой окружающей нас вселенной. И для таких существ как люди, наиболее эффективным оказалось воспринимать вселенную как трёхмерное окружение.
Представь себе 4 прямые, каждая из которых перпендикулярна остальным трём. Это и будет четырёхмерное пространство.
Опишу немного по другому.
Есть окружающая вселенная. Мы её воспринимаем как трёхмерную. Ничего не мешает ей быть 4-х мерной, 5-и мерной и т.д. до бесконечности. Ничего не мешает ей «быть» 2-х мерной, одномерной, нульмерной. Более интересно, можно ли её воспринимать «минус» трёхмерной.
Такая же чехорда со временем.
Время в привычном нам виде существует и зависит только от нашего восприятия.
Понятие времени можно расширить в зависимости от представления существования вселенной. Можно прийти к понятию плотности времени, разрывности времени, и обратного направления течения времени. Мало того, можно описать состояния, когда времени вообще, в любом виде не существует. Вселенная есть, а времени нет.
Однако точно ответить на вопрос о том, существуют ли 4D существа сегодня не может никто.
А как-же пространство-время и прочая физика? Мы и есть 4D-существа.
Тебя так каждое утро так штырит?
Проблема простых-близнецов – Алексей Савватеев | Научпоп
В чём заключается одна из самых древних проблем «школьной» математики? Почему она называется «простые-близнецы» и как формулируется? Что утверждает теорема о распределении простых чисел в натуральном ряду? Как продвинулась в этой области современная математика и на какие вопросы ещё предстоит найти ответы математикам будущего?
Рассказывает Алексей Савватеев, математик и матэкономист, доктор физико-математических наук, научный руководитель Кавказского Математического Центра АГУ, ректор Университета Дмитрия Пожарского, профессор МФТИ, научный руководитель ЦДПО РЭШ, ведущий научный сотрудник ЦЭМИ РАН, популяризатор математики среди детей и взрослых.
Молдавские учёные решили проблему, над которой 140 лет бились математики всего мира
Два математика из Молдовы первыми в мире решили алгебраическую проблему, над которой 140 лет размышляли великие ученые мира. Об этом на этой неделе сообщил Технический университет Молдовы (UTM).
«Доктор физико-математических наук Михаил Попа и доктор математических наук Виктор Прикоп первыми в мире нашли решение знаменитой проблемы центра и фокуса, поставленной выдающимся французским математиком Анри Пуанкаре, над которой великие математики мира размышляли более века», — говорится на сайте университета.
Этой проблеме посвятили тысячи работ математики из Франции, России, Беларуссии, Китая, Великобритании, Канады, США и других стран мира. Только в Молдове число работ, посвященных проблеме Пуанкаре, приближается к сотне, отметили в UTM.
Профессор университета Михаил Попа, основатель научной школы алгебры Ли и дифференциальных систем, предложил собственное решение проблемы центра и фокуса, которое привело его к результату, ставшему открытием.
Во время исследований к профессору присоединился его ученик Виктор Прикоп. Вместе они усовершенствовали первоначальную гипотезу в монографии «Проблема центра и фокуса. Алгебраические решения и гипотезы».
Работа была переведена на английский язык и представлена для издания в несколько зарубежных издательств. В итоге лучшие условия предложил издательский дом «Taylor & Francis Group», расположенный в Великобритании и специализирующийся на публикациях научной литературы и журналов.
Где-то всплакнул Гриша Перельман.
Панорама, да не та. И с такими лицами не шутят.
Что такое наука и какие задачи она должна решать? Существует ли музыкальная наука и какими могут быть результаты применения научного метода в этой сфере? Что такое микрохроматика и как она может изменить музыку будущего, расширить возможности её создания и восприятия?
История проблемы равенства классов P и NP
В 2000 году Математический институт Клэя определил 7 математических задач, решение которых не могли найти в течение многих лет. За решение каждой из них была назначена награда в размере 1 миллиона долларов. Эти 7 задач известны как «задачи тысячелетия», и на сегодняшний день только одна из них была решена — гипотеза Пуанкаре. В этой статье пойдет речь о вопросе равенства классов P и NP, ответ на который может сильно повлиять на всю IT-сферу.
Равенство P и NP классов отсылает нас к теории алгоритмов, а именно к классам сложности. Первое, с чего стоит начать, это то, что классы P и NP классифицируют языки, а не задачи. Пока что это звучит довольно абсурдно, поэтому для понимания разберемся в некоторых деталях.
Пусть А — алфавит и L ⊆ А*, тогда L называется языком над А. Для любого алфавита пустое множество и А* являются тривиальными языками. При этом пустое множество часто называют пустым языком. Однако не стоит путать пустой язык и язык, содержащий пустое слово e, — они различны. Языки могут быть как бесконечными, так и нет, но обязательно счетными. Т. е. множество всех действительных чисел языком нельзя назвать, т. к. такой набор является неисчисляемым.
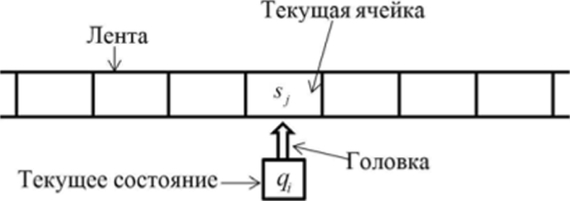
Говоря про абстрактный исполнитель, чаще всего имеют в виду машину Тьюринга, поэтому в дальнейшем под АИ будем подразумевать именно её. Итак, машина Тьюринга имеет неограниченное линейное хранилище, сгруппированное в ячейки. Каждая ячейка может содержать ровно один символ алфавита в любой момент времени. Вдоль ячеек идет считывающая головка, имеющая конечное число состояний. За одну итерацию она может считать значение только одной ячейки, переписать её значение, изменить свое состояние и перейти на одну позицию вправо/влево.
Устройство машины Тьюринга
На основе машины Тьюринга определим так называемую разрешающую машину над языком. Для начала введем определение характеризующей функции X(w). Функция X определяет, принадлежит ли слово w языку L. Если да, то значение функции равно «1»; если нет, то «0». Формально это можно записать так:
Разрешающей машиной D для языка L называется такая машина, которая для каждого w∈A вычисляет характеризующую функцию X(w) за конечное время.
В дополнение к разрешающей машине идет верификатор. Машина V, которая принимает слова w и c и выводит 0 или 1 после конечного числа шагов, называется верификатором для L, если она обладает следующими свойствами:
— выводит 1, только если w входит в язык L;
— для любого w в языке L существует такое c, что V(w,c) = 1.
Классы сложности и формулировка проблемы
Окей, мы рассмотрели несколько понятий. На первый взгляд, все это больше походит на лингвистику: алфавиты, слова, языки… Причем тут задачи? Чтобы ответить на этот вопрос, обратимся к понятию задача разрешимости (англ. Decision problem). Это такой вопрос (сформулированный в формальной системе), требующий ответа «да» или «нет», зависящего, возможно, от значений некоторых входных параметров. Например, «является ли данное натуральное число x простым?» или «даны два числа: x и y; делится ли x на y?« Метод решения в виде алгоритма называется разрешающей процедурой. Теория вычислимости имеет дело в основном с задачами разрешимости и приведенные выше конструкции наглядно соотносятся с таким типом задач: так разрешающая машина над языком является формализацией разрешающей процедуры. Но как же быть с задачами, такими как задача коммивояжера? На них нельзя дать бинарный ответ. В таких случаях применяют приемы приведения к версии decision problem. В случае коммивояжера проблема по-новому формулируется так: «существует ли маршрут не длиннее, чем заданное значение k?»
В класс сложности NP входят все языки L, для которых существует такой верификатор, что для каждого (w,c) время его работы полиномиально. Иными словами, NP включает в себя задачи разрешимости, для которых при подходящем сертификате для данного w мы быстро сможем удостовериться в том, что w действительно принадлежит L (ответ на вопрос можно довольно быстро проверить). Отсюда и название «верификатор». В качестве примера задачи в NP можно привести определение наличия в графе гамильтонова цикла. Сертификат в данном случае — последовательность вершин, образующих гамильтонов цикл.
Помимо этих классов можно выделить ещё 2: NP-hard и NP-Complete. Они основываются на приводимости одного языка к другому за полиномиальное время: пусть языки A и B — языки над одним алфавитом. Язык А будет приводимым за полиномиальное время к языку B, если существует такая функция f(w), что
— функция f может быть вычислена машиной Тьюринга за полиномиальное время.
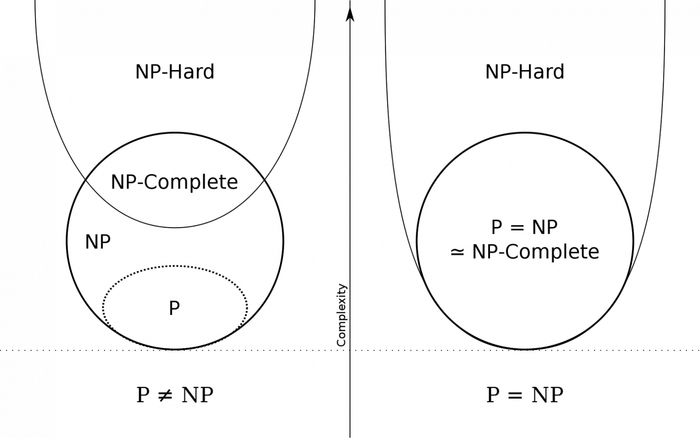
Тогда в класс NP-hard будут входить языки, к которым приводимы все языки в NP (причем NP-hard язык может входить в NP, а может и нет), а в NP-Complete те языки, которые являются одновременно NP-hard и NP. Примером NP-Complete является язык выполнимых булевых формул (SAT). Таким образом, NP-Complete задачи образуют в некотором смысле подмножество «типовых» задач в классе NP: если для какой-то из них найден «полиномиально быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
Отношение между классами при равенстве и неравенстве
Теперь, немного погрузившись в теорию алгоритмов, более конкретно обозначим проблему равенства данных классов. Итак, множество P входит в множество NP, но неизвестно, существуют ли языки, которые входят в NP и не входят в P. Что это означает на практике? Итак, простыми словами класс NP можно охарактеризовать как «трудно решить, легко проверить». Классическим примером задачи, входящей в NP, является задача коммивояжера, для решения которой на данный момент известен лишь один алгоритм — старый добрый перебор (мы не рассматриваем эвристические методы). Однако, получив ответ, его будет не так сложно проверить. Класс P же вобрал в себя те задачи, для которых существует эффективный алгоритм решения, позволяющий решать их за полиномиальное время. И равенство или, наоборот, неравенство этих классов пока не доказано. Если эти классы равны, то это будет значить, что для всех задач, которые сейчас решаются путем перебора или другим неэффективным методом, существует(-ют) полиномиальные алгоритмы. А если не равны, то придется смириться с неоптимальностью решения этих задач.
История проблемы равенства P и NP началась в 1928 году, когда Давид Гильберт сформулировал проблему, названную Entscheidungsproblem (нем. задача разрешения). Ее суть заключается в нахождении алгоритма, определяющего доказуемость данного утверждения из аксиом с использованием правил логики. По названию очевидно, что это задача является задачей разрешения (выводит «да» или «нет»).
В ходе решения этой проблемы потребовалось определить термины «алгоритм» и «вычислимая функция». В 1936 году Алонзо Чёрч и Алан Тьюринг независимо показали, что общее решение Entscheidungsproblem невозможно, предположив, что интуитивное понятие «эффективная вычислимость» соответствует вычислимости функции на машине Тьюринга. Эта гипотеза сегодня известна как тезис Чёрча-Тьюринга.
20 марта 1956 в письме к Джону фон Нейману Курт Гёдель впервые поставил вопрос о вычислительной сложности. Гёдель интересовался, можно ли получить доказательство теоремы (в математико-логическом смысле слова) за квадратичное или линейное время. К сожалению, письмо было обнаружено лишь в 1989 году и получило широкую огласку, когда Юрис Хартманис опубликовал перевод и комментарий.
Статья Алана Кобэма 1965 года под названием «The intrinsic computational difficulty of functions» является одним из первых упоминаний класса сложности P, состоящего из разрешимых за полиномиальное время задач. Тезис Кобэма-Эдмондса (известный также как расширенный тезис Чёрча-Тьюринга), названный в честь Алана Кобэма и Джека Эдмондса, утверждает, что любая разумная модель вычислений может быть выражена через другую модель с замедлением, не более чем полиномиальным по размеру входных данных. Кобэм предположил, что класс P может быть хорошим способом для описания множества реально вычислимых задач. Любая проблема, не содержащаяся в P, невозможна, но если задача реального мира может быть решена с помощью алгоритма, существующего в P, то такой алгоритм в конечном итоге будет открыт.
В 1965 году Юрис Хартманис и Ричард Стернс опубликовали статью «On the Computational Complexity of Algorithms», отмеченную премией Тьюринга. В ней даются более точные определения сложности алгоритма и класса сложности. Хартманис и Стернс определили класс сложности как совокупность всех задач, которые можно решить за установленные временные рамки. В их статье показано, что существует бесконечная иерархия классов сложности (например, задачи, для которых наиболее быстрый алгоритм имеет время, пропорциональное n, n log n, n^2, n^3, 2^n и т. д.), где небольшое увеличение временного интервала позволяет решать больше задач. Во второй статье Хартманис совместно с Филипом М. Льюисом показали, что подобная иерархия существует и для количества памяти (функция от размера входа) при решении задачи на машине Тьюринга.
В 1967 году Мануэль Блюм разработал аксиоматическую теорию сложности, которая основана на его собственных аксиомах (аксиомы Блюма), и получил важный результат — теорему об ускорении. До этого мы говорили по большей части о сложности алгоритма. Хотелось бы аналогичным образом определить и сложность задачи: например, какова сложность самого эффективного (по времени и емкости) алгоритма, решающего эту задачу. Теорема об ускорении гласит, что есть некоторые задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм.
Точная формулировка проблемы равенства P и NP была представлена в 1971 году. Тогда американский ученый Стивен Кук и работавший независимо советский ученый Леонид Левин доказали, что существуют практически актуальные проблемы, которые являются NP-полными. В США Стивен Кук опубликовал статью «The complexity of theorem proving procedures», в которой формализовал понятия редукции за полиномиальное время и NP-полноты, а также доказал существование NP-полной задачи (задача выполнимости булевых формул, SAT). Теорема была независимо доказана Леонидом Левиным и, таким образом, получила название «теорема Кука-Левина».
В 1972 году Ричард Карп сделал рывок в знаменитой статье «Reducibility among Combinatorial Problems», в которой показал, что около 20 разнообразных задач из комбинаторики и теории графов, известных своей вычислительной трудностью, являются NP-полными.
В августе 2010 года Виней Деолаликар, работавший в исследовательском отделении Hewlett-Packard в Пало-Альто в Калифорнии, заявил, что разгадал загадку P vs NP. Он утверждал, что P не равняется NP, однако научное сообщество нашло в его доказательстве фатальную ошибку. В начале 2002 года SIGACT News провел опрос среди 100 ученых, задав им вопрос о равенстве классов NP и P. 61 человек ответили, что «неравны», 9 — «равны», 22 затруднились ответить и 8 сказали, что гипотеза не выводима из текущей системы аксиом и, таким образом, не может быть доказана или опровергнута.
К чему приведет решение проблемы
Окей, теория вычислимости, формализация алгоритмов и абстрактные математические теории — все это конечно интересно, но как решение проблемы равенства NP и P классов отразится на практике? На самом деле, алгоритмы для решения NP-задач используются каждый день во многих сферах. Например, в криптографии, криптовалютах, восстановлении поврежденных файлов, системах блокировки спама, оптимизации в логистике и т. д. Более эффективные решения могли бы значительно сэкономить время и деньги, так как мы пользуемся в основном эвристическими методами, дающими лишь приближенные решения.
Однако существует и обратная сторона монеты. Солидная часть криптографии (криптосистемы с открытым ключом, технологии доказательства выполнения работы в блокчейне, системы блокировки спама) основывается на предположении о неравенстве NP и P классов. Если окажется, что некоторые задачи, для которых, как считалось, не существует эффективных алгоритмов, можно решать быстро, то многие методы защиты устареют.
Может оказаться и так, что последствия решения окажутся не такими тривиальными, как это часто и бывает в математике. В качестве примера рассмотрим континуум-гипотезу о существовании мощности, меньшей континуума и большей мощности счетного множества. Оказывается, существование такого кардинала нельзя ни доказать, ни опровергнуть в аксиоматике ZFC. Так что мы вправе считать, что такие мощности бывают (впрочем, как и считать, что не бывают). Однако ясно, что мы не можем конструктивно построить соответствующее множество. Возможно, точно также окажется и с алгоритмами для NP-задач в случае равенства NP и P (к слову, некоторые математики в опросе SIGACT News так и ответили: гипотеза не выводима из существующей системы аксиом, то есть не может быть доказана или опровергнута).
Пока что существующих методов доказательств недостаточно для строго математического ответа, но не нужно терять надежду. В марте 2001 года Ричард Карп предсказал, что проблема будет решена молодым математиком (до 30 лет) с использованием подхода, о котором еще никто не думал. Стивен Кук заявил, что кто-нибудь предоставит убедительное доказательство в ближайшие 20 лет.
Реставрирую шкаф
Работа не быстрая, поэтому фото до. Нашел в нем тайник, в тайнике фото.
Интересует, что за формула на доске?
Пока ответа не нашлось.
Шкаф в СПБ. Ещё была найдена карта Казани печать старая начало 20 века.
Что, если наш 4D мир станет пятимерным?
Краткая текстовая версия видео:
Мир, в котором мы живем, является четырехмерным. По крайней мере в макро масштабе. В нашем мире 3 пространственных измерения и одно временное. Трехмерность пространства значит, например, то, что мы можем в нем провести три взаимно перпендикулярных координатных осей расположенных под углом 90 градусов. В таком пространстве можно двигаться «влево-вправо», «вперед-назад» и «вверх-вниз».
В трехмерном пространстве мы можем завязать узел. В двумерном пространстве завязать узел невозможно. А еще в трехмерном пространстве стул может стоять только на трех ножках или больше, стул на двух ножках потеряет равновесие и упадет (Речь идет о ножках типа такого, как на фото).
А что будет, если мы добавим еще одно пространственное измерение? То есть представим себе пятимерный мир, 4 пространственных измерения и 1 временное?
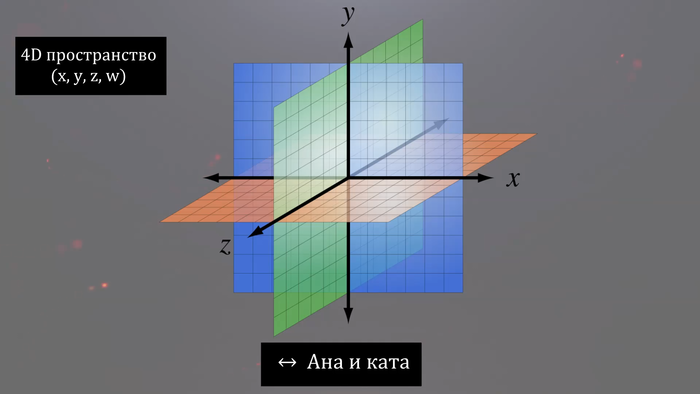
В таком мире можно провести еще одну ось перпендикулярную к остальным трем осям под углом 90 градусов. В трехмерном пространстве сделать это невозможно и как-то точно визуализировать я это не могу, так что включайте фантазию.
В пятимерном мире так же добавятся новые направления движения, которые называют «ана-ката», получается: «влево-вправо», «вперед-назад», «вверх-вниз» и «ана»-«ката». Представить себе направление движения ана и ката мы не можем, так же как существо в двумерном мире не может представить себе направления вверх и вниз.
В таком мире можно завязать двумерную сферу на узел, в нашем мире сделать это невозможно, показать, соответственно, тоже нельзя. Ну и стул с тремя ножками не сможет стоять в мире с 4 пространственными измерениями, чтобы он был устойчив потребуется 4 или больше ножек.
Ну хорошо, я понимаю, вы вряд ли Вы читаете это, чтобы узнать о узлах и ножках стула, Вас интересует, что будет с нашим миром, если внезапно в него добавить еще одно измерение, вот так по щелчку пальца «тыц» и добавили еще одно пространственное измерение и вот ты уже в 5 измерении, что с тобой будет?
Если коротко то… умрешь конечно же. А еще Земля станет приплюснутой. Сейчас расскажу как именно умрешь и почему земля станет приплюснутой.
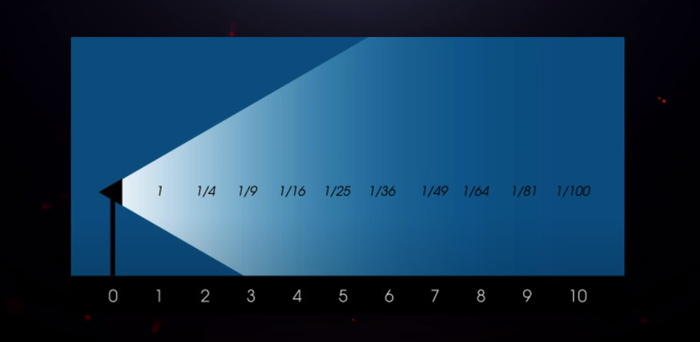
Есть такой закон – закон обратных квадратов, и он тесно связан с размерностью пространства. Возьмем для примера светящий фонарь, интенсивность света в таком случае убывает согласно закону обратных квадратов.
Объект, перемещенный на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении. На расстоянии в 3 раза большее от источника – в 9 раз меньше мощности, на расстоянии в 4 раза большее от источника – 16 раз и так далее.
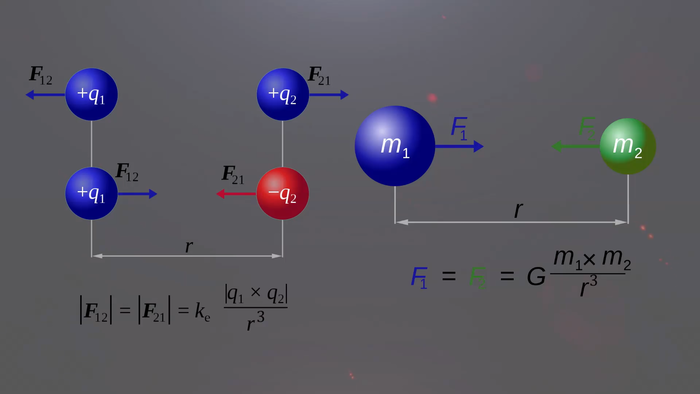
В законе всемирного тяготения сила гравитационного притяжения убывает тоже с квадратом расстояния. В два раза увеличиваем расстояние, сила притяжения уменьшается в 4 раза и так далее. Тоже самое с законом Кулона – сила притяжения или отталкивания заряженных частиц убывает с квадратом расстояния. В 5D мире закон обратных квадратов превращается в закон обратных кубов. Теперь интенсивность света будет падать не с квадратом расстояния, а с кубом расстояния. r^2 в законе Кулона и Законе всемирного тяготения превращается в r^3.
Это все полностью изменит химические элементы из которых мы состоим, некоторые атомы станут нестабильными, радиоактивными, другие наоборот, станут стабильными.
Например, в 5D мире магний был бы благородным газом, а не металлом, то есть некоторые элементы станут менее реактивными, другие более реактивными. Ионизация атомов будет осуществляться при значительно меньших энергиях, да и вообще агрегатное состояние различных элементов будет меняться не так, как в нашем мире, некоторые хим. элементы станут газообразны при комнатной температуре, некоторые затвердеют и такие вот вещи. Думаю, практически бессмысленно вспоминать биологические процессы, благодаря которым мы можем жить, ведь это все поменяется кардинально, мы мгновенно потеряем сознание и умрем, синтез белков, транспортировка различных аминокислот, нейромедиаторов, нервные импульсы, это все либо прекратится, либо изменится до неузнаваемости. Ну и конечно же спектры атомов изменятся, а это значит, что все резко поменяет цвет, что-то станет прозрачным, что-то непрозрачным, да и вообще привычные для нас источники света выглядели бы более тускло из-за r^3, с запахами та же история, правда уже некому будет смотреть и нюхать все это, ведь все живые существа погибнут.
Короче будет происходить полная жесть, что-то будет плавится, что-то превратится в газ, что-то затвердеет, некоторые вещества станут радиоактивными, привычные нам вещи потеряют свои свойства и перестанут работать так, как в нашем мире. Я напомню, что это все в мире, в котором 4 пространственных измерения и одно временное и в котором можно двигаться в направлении ана и ката. Но кроме дополнительного направления появятся также дополнительные степени свободы во вращении. В нашем мире ориентацию тела можно задать тремя углами, в быту это называется «наклон, подъём и поворот», в 5D мире надо представить себе еще 3 дополнительных степени свободы вращения перпендикулярные к 3 вышеупомянутым. Но по идее, на вращение Земли это не должно повлиять, момент импульса сохранится, ведь нужно, чтобы какая-то сила передала момент импульса Земле, чтобы она могла вращаться в какой-то непривычный для нас способ. Конечно Земля изменит свой привычный облик, из-за того, что свойства химических элементов изменятся, но из-за гравитации все должно также удерживаться вокруг центра масс, правда земля довольно быстро вращается, а так как гравитация в 5D мире у нас ослабевает с кубом расстояния, то земля сплюснется и формой будет напоминать что-то типа такого, как на картинке.
Но вообще, появится дополнительное направление, в котором могут двигаться частицы из которых состоит земля, планета начнет превращаться в гиперсферу, представить себе этот процесс, эти метаморфозы которые будут происходить, очень сложно.
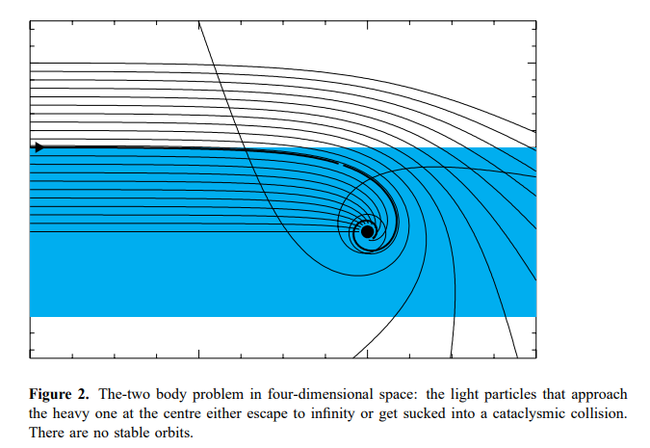
Будут ли происходить термоядерные реакции на солнце, тут под вопросом, но изменения явно произойдут. Но вот что забавно – в пятимерном мире нет стабильных орбит. Вот, посмотрите на график, это моделирование классической задачи двух тел, оказывается, что устойчивых орбит в 5D мире нет, тела либо падают друг на друга, либо улетают в бесконечность, поэтому солнечная система, как и все другие системы, разрушится, некоторые тела упадут на другие тела, а некоторые улетят бороздить просторы галактики.
Казалось бы, следуя логике как с законом обратных квадратов, все квадраты в других уравнениях тоже надо заменить на кубы и получается, что формула эквивалентности массы и энергии в пятимерном пространстве будет работать как Е=мс в кубе, но нет, эта формула, как и множество других, не изменятся в пятимерном пространстве, она, как и множество других формул, не зависит от размерности пространства.
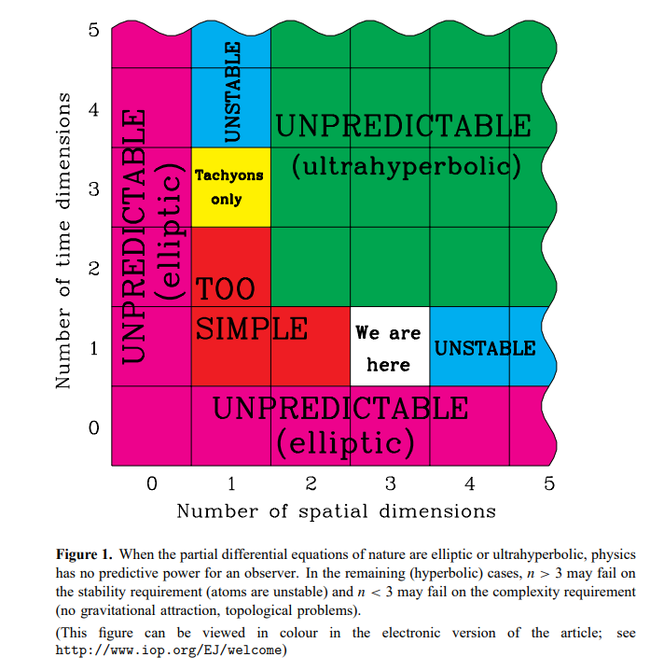
Но даже и без этого всего, мир в 5 мерном пространстве изменится настолько, что в нем не сможет существовать жизнь в том виде, в котором существует в четырехмерном пространстве. Вообще, оказывается, четырехмерный мир – самый простой из возможных и одновременно самый оптимальный для существования в нем жизни, стабильных орбит и химии, какой мы ее знаем.
Книга Кипа Торна, «Интерстеллар. Наука за кадром»
Единственный в своём роде треугольник Шарыгина, открытый лишь в 1982 году
Приветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать об удивительном геометрическом объекте, впервые рассмотренным советским математиком Игорем Федоровичем Шарыгиным.
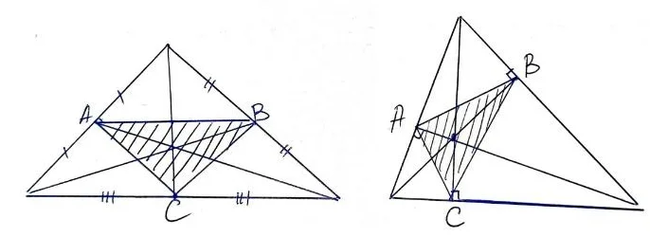
Для начала посмотрите на рисунок ниже. Что Вы на нём видите?
Но, погодите, есть же еще биссектрисы!
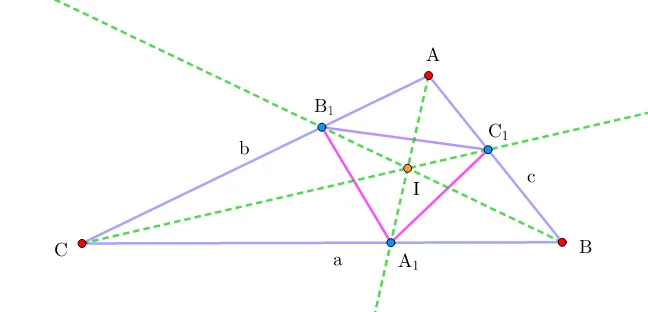
И тут становится интересно! Оказывается, и это показал Игорь Федорович, полученный из биссектрис треугольник может быть равнобедренным!
Заметка Шарыгина об этом объекте опубликована в книге «Задачи по геометрии. Планиметрия», 1982.
Впрочем, есть одно очень тонкое условие: угол такого треугольника должен попадать в диапазон от 102,663 до 104,478 градусов!
Основная суть доказательства сводится к рассмотрению подобных треугольников и применению теоремы косинусов, что позволяет получить вот такие выражения для сторон треугольника:
Самим доказательством (доступным каждому школьнику 9 класса!) можно проникнуться в телеграмм-канале «Математика не для всех».
Математика
Старение и бессмертие: взгляд биолога
Данная заметка написана по просьбе комментатора.
Когда я обучался в магистратуре, нам читал лекции профессор Валерий Степанович Тырнов, исследователь старения. Натура увлечённая, он рассказывал немало удивительного. Например, о том, что обнаружил на сыре штамм плесени, способный расти при отрицательных температурах, который содержит в морозилке, несмотря на протест жены. Профессор надеялся принять с этим штаммом участие в экспериментах, изучающих возможности терраформирования Марса. Ещё он рассуждал о внедрении в геном человека генов, отвечающих за фотосинтез, с целью получения «зелёных человечков», питающихся солнечным светом. Когда я сдавал экзамен профессору, у него уже отказывало зрение. В следующем семестре Валерий Степанович умер. Он пытался успеть победить старение, но не успел. Рассуждая вслух, Валерий Степанович говорил, что первый заметный признак старения у человека проявляется очень рано, зачастую – в подростковом возрасте. Это – кариес постоянных зубов.
Говоря о старении и естественной смерти, мы имеем в виду, прежде всего, многоклеточных животных. Среди одноклеточных и растений явления старения и смерти весьма размыты. Да, согласно новым научным данным, существует т.н. клональное старение штаммов микроорганизмов: для одних существует ограниченное количество делений митозом (бесполое размножение), для других биологические часы обнуляются лишь в одной из разделившихся половинок. Это т.н. репликативное старение. Многие исследователи говорят о хронологическом старении самих клеток простейших организмов. Но это лишь с одной стороны. С другой стороны, теоретически бессмертны растения, размножающиеся вегетативно. Кто может сказать, сколько лет существует традесканция, высаженная в горшок черенком, отделённым от традесканции из другого дома, и та, в свою очередь, когда-то была черенком… Это всё один и тот же геном, один и тот же индивидуум, с генетической точки зрения. В центре пустыни Мохаве произрастает King Clone – клональная колония креозотового куста (Larrea tridentata), возраст которой оценивается в 11700 лет.
Наблюдения за гигантскими груперами (Epinephelus lanceolatus), длиной 2,5 м. и весом до 400 кг. (живут 100-120 лет) показали, что старые особи проигрывают конкуренцию молодым. Они менее поворотливы из-за огромных размеров, зачастую не имеют возможности спрятаться в пещеру. Но они не стареют. Они по-прежнему отлично видят малейшее шевеление усика креветки из-под дальнего камня. Они просто перерастают свою экологическую нишу.
Максимальная продолжительность жизни человека – 120 лет.
Теперь попробуем классифицировать современные теории старения. Во-первых, следует выделить 2 большие группы эволюционных теорий старения.
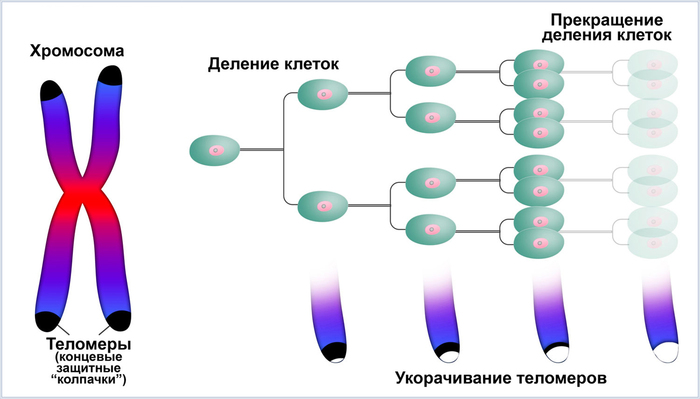
Весьма популярны ныне теории, связанные с т.н. лимитом (пределом) Хейфлика. Такова теломерная теория Оловникова. В соматических клетках с диплоидным набором хромосом размеры теломер (участков ДНК на концах хромосом) с каждым делением клетки сокращаются, по причине отсутствия фермента теломеразы в клетке. Когда теломеры станут достаточно коротки, ДНК-полимераза потеряет способность реплицировать концы молекулы ДНК. Включается процесс апоптоза – запрограммированного саморазрушения клетки. Так, предельное число делений для клеток человеческого организма – 52 деления.
Клетки, в которых функционирует теломераза – бессмертны. Таковыми являются половые и раковые клетки. Полагается, что теломераза исчезла в соматических клетках не случайно, а для подавления опухолеобразования.
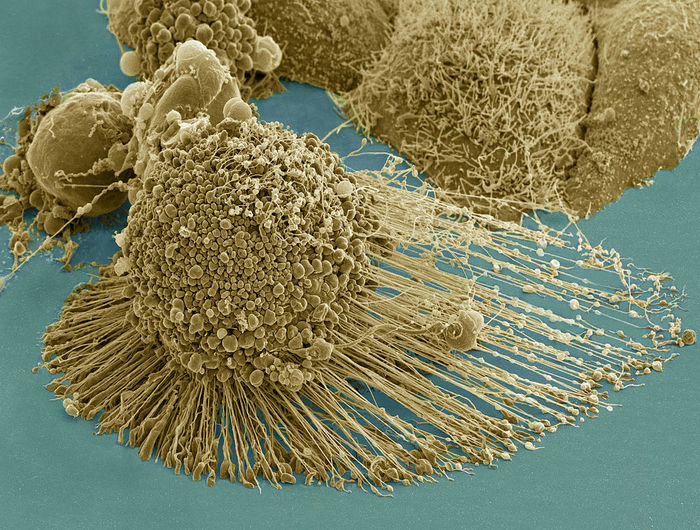
Линия клеток HeLa из раковой опухоли шейки матки пациентки по имени Генриетта Лакс, умершей в 1951 г, считается бессмертной. В декабре 1960 года клетки HeLa первыми полетели в советском спутнике. В 1968 г. на борту советского космического аппарата «Зонд-5» они облетели вокруг Луны. Эти клетки эволюционировали за прошедшие годы. Иногда они способны заражать культуры других клеток. Лен Ван Вален описал эти клетки как новый вид организмов – Helacyton gartleri, впрочем, обычно биологи не относятся к последнему всерьёз.
Рассмотрим теперь теории, рассматривающие старение как следствие повреждения клеток. Это вторая группа теорий старения.
Действительно: в мире стареет всё. Изнашивается ботинок, точит вода камень, солнца превращаются в красные гиганты… Эта группа теорий старения рассматривает старение как результат отсутствия программы репарации и способна вызвать некоторый психологический дискомфорт. Ведь написать программу это совсем не то, что просто её удалить, не так ли?
Рассмотрим одну из таких теорий, т.н. теорию накопления мутаций. Согласно этой теории, предложенной Питером Медаваром в 1952 году, естественный отбор препятствует накоплению вредных мутаций, проявляющихся до возраста, достижение которого необходимо организму для реализации репродуктивных функций. Далее действие естественного отбора ослабевает, и накопившиеся вредные мутации, проявляющиеся после прохождения организмом репродуктивного цикла, обеспечивают феноменологию старения. Очевидно, что домовой мыши с быстрым метаболизмом, маленьким тельцем и быстрым репродуктивным циклом, долгая жизнь ни к чему, другое дело – огромный слон, которому необходимо выносить слонёнка. Не отвергая ценного наблюдения о существовании некоторой корреляции между длиной репродуктивного цикла и продолжительностью жизни, отметим, что на настоящий момент теория накопления мутаций остаётся гипотезой.
Гораздо ближе автору этих строк т.н. теория одноразовой сомы. Согласно этой теории, в процессе эволюции стоял вопрос об ограниченности ресурсов. Ресурсы могли быть потрачены на репарацию, а могли быть потрачены на другие функции. В итоге они были потрачены на репарацию (восстановление) ровно на столько, сколько необходимо для реализации репродуктивного цикла. Поскольку жизнь это эволюция нуклеиновых кислот… И природа любит оптимизацию: у полихет – множество параподий, у их потомков членистоногих число ног с повышением уровня организации сокращается. У речного рака 5 пар ходильных ног, у паука – 4, у насекомых – 3, а клопу водомерке для прыжков по воде достаточно 2 пары, 3-я пара передних лапок – специализирована. В целом, данный взгляд на эволюцию старения разделяется основной частью биологического сообщества.
Однако, эволюционные теории старения рассматривают этот процесс в самых общих чертах. Отдельной категорией следует отметить теории старения, рассматривающие конкретные механизмы старения. Одну такую теорию (связанную с пределом Хейфлика) мы уже рассмотрели. Другая подобная теория – свободнорадикальная теория старения. Она утверждает, что старение происходит из-за накопления в клетках повреждений, нанесённых свободными радикалами с течением времени. Свободными радикалами называются молекулы или атомы, содержащие один или несколько неспаренных электронов на внешнем электронном уровне. Очевидно, что в основе этой теории во многом лежит эмпирическое наблюдение: животные с интенсивным метаболизмом живут меньше, чем животные с медленным метаболизмом. Сравните землеройку и черепаху. Одна из модификаций свободнорадикальной теории – митохондриальная теория старения, отводящая ключевую роль в процессе таким органоидам клетки, как митохондрии. Вряд ли свободные радикалы являются единственной причиной старения, однако, не следует забывать, что данный подход предполагает возможность увеличения продолжительности жизни при соблюдении определённой диеты (низкокалорийной) и регулярных занятиях спортом.
Автор этих строк придерживается взгляда, что старение связано с множеством механизмов. По аналогии с ботинком: он стирается, и одновременно у него может отклеиваться подошва. Это т.н. системный подход к старению, разделяемый большинством биологов.
Человек мечтает о вечной молодости и бессмертии с тех пор, как осознал себя смертным. Николай Фёдоров, предтеча и вдохновитель Циолковского, мечтал о воскрешении в будущем всех, когда-либо живших, силами науки. Эта идея не так утопична, как может показаться на первый взгляд, если учесть, что человеческий разум трансформирует в природе всё, с чем не может смириться. Люди не могли смириться с тем, что не способны летать, и, в конце концов, создали летательные аппараты. Может ли человек смириться со смертью близких? Нет.
Однако, сейчас нас интересует лишь остановка старения: существует ли в природе радикальный механизм омоложения? Доктор биологических наук Николай Мушкамбаров считает, что таким механизмом является мейоз – процесс образования половых клеток, известный каждому из школьных учебников биологии.
И вот тут нам придётся вступить в область научной фантастики.
Механизм обнуления биологических часов существует, и этот механизм воспроизводится в процессе полового размножения. Однако, обновлённый организм отличается от исходных родительских, но главное – занимает отдельное, искривлённое по Вернадскому, пространство. Даже если мы говорим об эмбрионе в теле матери. Доктор Мушкамбаров рассуждает о возможности запустить необходимые для обновления процессы мейоза в соматических клетках, нужно только полностью определить гены, ответственные за разные аспекты мейоза. Конечно, Мушкамбаров, оговаривается, что пока речь идёт о фантастическом проекте.
Однажды я беседовал обо всём этом со специалистом по старению (на тот момент – кандидат наук, преподаватель МГУ). Он отвечал, что его мысли движутся в том же направлении.
Тут возникнет множество этических противоречий. Подобная власть над биологической природой означает утрату смысла не только для таких понятий как возраст, пол, раса, внешний облик (всё это окажется легко трансформируемым в течение жизни), но и для привычных нам всем свойств человеческого организма (вспомните зелёных человечков профессора Тырнова, или человека-амфибию Беляева). Да, это философия трансгуманизма. Не цифровой трансгуманизм (киборгизация или оцифровывание человека, что мне неприятно), но биологический. Однако, прежде чем пугаться, задумайтесь над тем, что трансгуманистические преобразования начинаются ещё тогда, когда первобытный человек впервые применил зубный протез. Вопрос лишь в мере…
Вдумайтесь, как мало живёт человек. Если вы увлекаетесь историей, палеонтологией, фантастикой, следите за политическими событиями, вам должно быть знакомо это чувство: вы никогда не узнаете, что будет через двести, тысячу лет… Не увидите смены формаций, не увидите новой, посткайнозойской эры… Не узнаете, есть ли жизнь в пределах иных звёздных систем. При том, что можете свободно перемещаться в воображении сквозь тысячелетия и эоны в прошлое. Доживём ли? Я считаю, что шанс дожить до ощутимого продления срока жизни у нас есть, а там глядишь, и. Конечно, увеличение численности населения предполагает освоение дальнего космоса.
Фридрих Энгельс полагал свободу осознанной необходимостью и говорил о скачке из царства необходимости в царство свободы. Именно о таком прыжке в царство биологической свободы, при условии познания биологических необходимостей, идёт речь. Ещё буддистские философы мечтали остановить колесо Сансары, бесконечный круговорот рождений, страданий и смертей. Жизнь в древней Индии была настолько тяжела, что эта остановка мнилась мрачным для современного человека способом: уходом в абсолютное небытиё. Когда я однажды впервые воспроизвёл биуретовую реакцию на белок в лаборатории, то вдруг осознал, что в этом и заключается конечный смысл науки биологии: остановить колесо, и каждая установленная учёными реакция, позволяющая идентифицировать те, или иные биологические молекулы, подобная этой, окрашивающей содержимое пробирки в лиловый цвет, каждая новая формула, приближает человечество к этому часу. Майский ветер с запахом пыльцы врывался в раскрытое окно, хотел бы я вновь пережить эту гамму чувств…
В заключение отмечу вот что. Рыночная экономика не заинтересована в индивидуальной эволюции и бессмертии каждого. Подобно тому, как биологическая эволюция заинтересована лишь в продлении рода, она заинтересована в умножении прибыли. Подумайте об этом.