Что такое штрих шеффера
Штрих Шеффера
Штрих Ше́ффера — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Генри Шеффером в 1913 г. (в отдельных источниках именуется как Пунктир Чулкова)
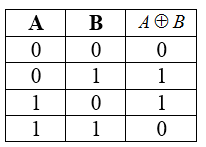
Штрих Шеффера, обычно обозначаемый |, задаётся следующей таблицей истинности:
| X | Y | X|Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Таким образом, высказывание X | Y означает, что X и Y несовместны, т.е. не являются истинными одновременно. От перемены мест операндов результат операции не изменяется.
Штрих Шеффера, как и стрелка Пирса, образует базис для пространства булевых функций от двух переменных. То есть используя только штрих Шеффера можно построить остальные операции. Например,




В электронике это означает, что для реализации всего многообразия схем преобразования сигналов, представляющих логические значения, достаточно одного типового элемента. С другой стороны, такой подход увеличивает сложность реализующих логические выражения схем и тем самым снижает их надёжность. Примером может являться промышленная 155 серия.
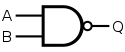
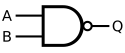
Элемент, реализующий штрих Шеффера обозначается следующим образом (по стандартам ANSI):
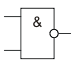
В европейских стандартах принято другое обозначение:
См. также
Литература
Полезное
Смотреть что такое «Штрих Шеффера» в других словарях:
ШЕФФЕРА ШТРИХ — логическая операция, обычно обозначаемая |, к рая задается следующей истинностной таблицей: Таким образом, высказывание означает, что Аи Внесовместны, т. е. не являются истинными одновременно. Через Ш. ш. выражаются все другие логич. операции.… … Математическая энциклопедия
Аксиома Вольфрама — является результатом исследований, осуществленных Стивеном Вольфрамом[1] в поиске кратчайшей аксиомы из одного уравнения, эквивалентной аксиомам булевой алгебры (или логике высказываний). Результатом[2] его поиска стала аксиома с шестью… … Википедия
Булева функция — В данной статье или разделе имеется список источников или внешних ссылок, но источники отдельных утверждений остаются неясными из за отсутствия сносок … Википедия
ЛОГИКА ВЫСКАЗЫВАНИЙ — раздел логики, в котором изучаются истинностные взаимосвязи между высказываниями. В рамках данного раздела высказывания (пропозиции, предложения) рассматриваются только с т.зр. их истинности или ложности, безотносительно к их внутренней субъектно … Философская энциклопедия
Логические операции — логические связки, логические операторы, функции, преобразующие высказывания или пропозициональные формы (т. е. выражения логики предикатов (См. Логика предикатов), содержащие переменные (См. Переменная) и обращающиеся в высказывания при… … Большая советская энциклопедия
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
Стрелка Пирса — Стрелка Пирса бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880 1881 г.г. Стрелка Пирса, обычно обозначаемая ↓, задаётся следующей таблицей истинности:… … Википедия
Логические элементы — Логические элементы устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого «1» и низкого «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике,… … Википедия
Битовая операция — Битовые операции, иногда также булевы или логические операции[1] операции над битами, применяемые в программировании и цифровой технике, изучаемые в дискретной математике и математической логике. Содержание 1 Введение 1.1 … Википедия
Булевы операции — Битовые операции, иногда также булевы или логические операции[1] операции над битами, применяемые в программировании и цифровой технике, изучаемые в дискретной математике и математической логике. Содержание 1 Введение 1.1 … Википедия
Штрих Шеффера
Из Википедии — свободной энциклопедии
Штрих Шеффера, обычно обозначаемый | или ↑, эквивалентен операции И-НЕ [1] и задаётся следующей таблицей истинности:
| X | Y | X | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Таким образом, высказывание X | Y означает, что X и Y несовместны, то есть не являются истинными одновременно. От перемены мест операндов результат операции не изменяется.
Штрих Шеффера, как и стрелка Пирса, образует базис для пространства булевых функций от двух переменных. То есть, используя только штрих Шеффера, можно построить остальные операции. Например,
В электронике это означает, что для реализации всего многообразия схем преобразования сигналов, представляющих логические значения, достаточно одного типового элемента. С другой стороны, такой подход увеличивает сложность реализующих логические выражения схем и тем самым снижает их надёжность. Примером может являться промышленная 155 серия.
Элемент 2И-НЕ (2-in NAND), реализующий штрих Шеффера, обозначается следующим образом (по стандартам ANSI):
В европейских стандартах принято другое обозначение:
Логические операции и их свойства
Вы будете перенаправлены на Автор24
Конъюнкция или логическое умножение (в теории множеств – это пересечение)
Конъюнкция является сложным логическим выражением, которое истинно в том и только том случае, когда оба простых выражения являются истинными. Такая ситуация возможно лишь в единственном случае, во всех остальных случаях конъюнкция ложна.
Таблица истинности для конъюнкции
Дизъюнкция или логическое сложение (в теории множеств это объединение)
Дизъюнкция является сложным логическим выражением, которое истинно практически всегда, за исключением, когда все выражения ложны.
Таблица истинности для дизъюнкции
Готовые работы на аналогичную тему
Отрицание, логическое отрицание или инверсия (в теории множеств это отрицание)
Таблица истинности для инверсии
Импликация или логическое следование
Таблица истинности для импликации
Эквивалентность или логическая равнозначность
Таблица истинности для эквивалентности
Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
Строгая дизъюнкция истинна, если значения аргументов не равны.
Таблица истинности для операции сложения по модулю два
Свойства строгой дизъюнкции:
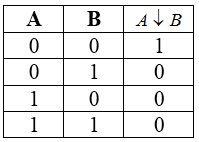
Стрелка Пирса
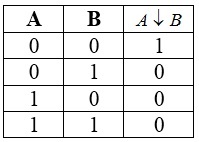
Таблица истинности для стрелки Пирса
Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:
$X \downarrow X = ¬X$— отрицание
$(X \downarrow Y) \downarrow (X \downarrow Y) \equiv X \vee Y$ — дизъюнкция
$(X \downarrow X) \downarrow (Y \downarrow Y) \equiv X \wedge Y$ — конъюнкция
$((X \downarrow X) \downarrow Y) \downarrow ((X \downarrow X) \downarrow Y) = X \to Y$ — импликация
В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).
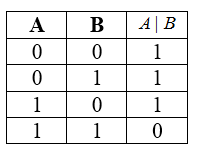
Штрих Шеффера
Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.
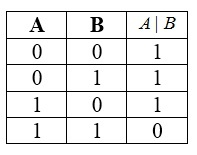
Таблицей истинности для функции штрих Шеффера
Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,
$X \mid X = ¬X$ — отрицание
$(X \mid Y) \mid (X \mid Y) = (X \wedge Y)$ — конъюнкция
$(X \mid X) \mid (Y \mid Y) = X \vee Y$ — дизъюнкция
Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Порядок выполнения логических операций в сложном логическом выражении
Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.
Общие свойства
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата написания статьи: 24 03 2016
Основные логические операции
Логические операции в создании компьютерных программ — действия, которые производятся над входными данными. Такие функции производятся над сигналами булевского типа, то есть над примитивными выражениями, имеющими только два возможных значения: истина или ложь.
Виды операций
В программировании выделяют следующие виды функций:
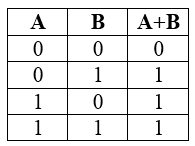
Логическое умножение (конъюнкция)
Конъюнкция — это действие, в результате которого каждым двум входным данным соответствует одно новое высказывание. Истинное значение на выходе получается, когда оба входных значения истинны.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
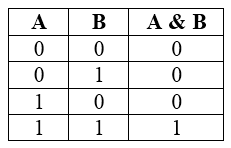
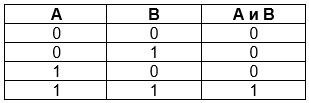
Таблица истинности для логического умножения выглядит так:
A, B — исходные данные;
A и B — значение, приобретаемое в результате реализации конъюнкции.
Из таблицы следуют свойства логического умножения:
Логическое сложение (дизъюнкция)
Дизъюнкция — это булева функция, в итоге которой выходные данные будут ложными только при ложности всех исходных выражений.
Таблица истинности логического сложения:
A, B — входная информация;
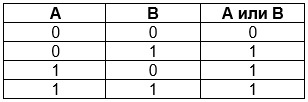
A или B — значение, приобретаемое в результате выполнения дизъюнкции.
Для дизъюнкции справедливы следующие утверждения:
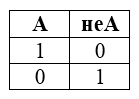
Логическое отрицание (инверсия)
Инверсия — выражение, ставящее в соответствие одному значению противоположное.
Условное обозначение логического отрицания: с помощью частицы «не», символов ¯, \(\neg.\)
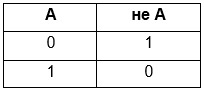
Таблица истинности инверсии:
A — исходные данные;
не A — значение, приобретаемое в результате логического отрицания.
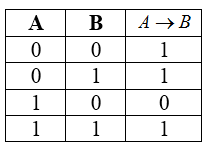
Логическое следование (импликация)
Импликация — это булева операция, ложная лишь тогда, когда первая исходная переменная является истиной, а вторая — ложью.
Следование записывается с помощью знака \(\rightarrow.\)
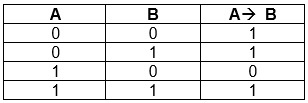
Таблица истинности для импликации:
A — входная информация, означающая условие;
B — входная информация, означающая следствие;
A → B — значение, приобретаемое в результате импликации.
По своему употреблению данная связка схожа со значением союзов «если. то. ».
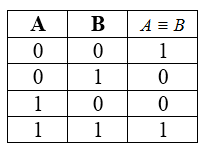
Логическая равнозначность (эквивалентность)
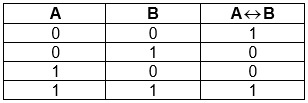
Эквивалентность — выражение, являющееся истинным лишь в случае равенства двух входных элементов.
Таблица истинности для равнозначности:
Стрелка Пирса
Стрелка Пирса — двухместное логическое действие со следующей последовательностью: сначала над исходными показаниями производится дизъюнкция, затем происходит отрицание полученного результата.
Данная манипуляция является отрицание логического сложения. Свое название рассматриваемая функция получила от своего автора — американского ученого Чарльза Пирса.
Таблица истинности для этой операции следующая:
Особенность стрелки Пирса заключается в ее возможности строить другие булевы функции.
Пример
Штрих Шеффера
Штрих Шеффера — это действие, приводящее к ложному итогу лишь при истинности обоих исходных данных. По порядку выполнения операций эта функция эквивалентна отрицанию конъюнкции.
Символ Шеффера назван по фамилии своего создателя — американского логика Генри Шеффера — и обозначается посредством знака \(\vert.\)
Таблица истинности для данной функции:
С помощью штриха Шеффера можно воспроизвести другие логические манипуляции.
Пример
Порядок выполнения операций
В составном логическом выражении действия выполняются в такой последовательности:
Для построения нужного порядка, как и в математических выражениях, используют скобки.
Штрих Шеффера



Эта операция обозначается знаком / и определяет несовместимость высказываний. Эта операция ложна тогда и только тогда, когда оба операнда истинны. Выражение «А/В» читается так: « 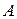
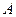 | 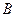 | 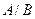 |
Например: «2 * 2 = 4» и «2 * 2 = 5» несовместны – это истинное высказывание;
«2 * 3 = 6» и «3 * 2 = 6» несовместны – это ложное высказывание, так как вот эти то высказывания как раз совместны.
Через базовые операции штрих Шеффера выражается так:
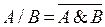
Поэтому эту операцию еще часто называют антиконъюктивной.
Эта операция интересна тем, что используя ее одну, можно выразить все остальные связки (операции) логики высказываний. Шеффер показал это, и используя эту единственную связку, построил свое исчисление высказываний. Покажем некоторые формулы перехода в это исчисление.
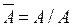
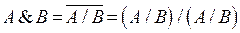
Упражнение. Выразите через штрих Шеффера оставшиеся логические операции (дизъюнкцию, импликацию, эквивалентность, исключающее или).
Ограничимся этим набором логических операций. Существует всего 16 двуместных операций. Выпишем их.
| A | B | A&B | AÞB | BÞA | AÅB | AÚB | A↓B | A↔B | ØB | B→A | ØA | A→B | A/B |
Все эти функции называют элементарными. Символы операций часто называют логическими связками.
Теорема. Число всех различных n-местных булевых функций равно 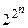
Пример, в котором появляются булевы функции.
Составным элементом нервной системы является нейрон. Это устройство предназначено для того, чтобы не пропускать слабые возбуждения и передавать достаточно регулярные и сильные.
Одна из моделей нейрона. Нейрон N имеет n входов, по которым в некоторый момент времени t могут поступать или не поступать возбуждения. Если в момент t более h входов возбуждены, на выход нейрона поступает возбуждение, в противном случае оно не поступает. Обозначим входы нейрона 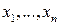
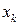
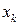
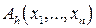
Будем считать, что 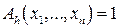
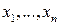
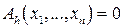
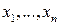
Для 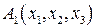
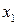 | 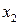 | 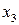 | 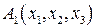 |
Теперь приведем несколько парадоксальных примеров, и подчеркнем, что истинность или ложность сложного высказывания зависит только от истинности или ложности элементарных высказываний, входящих в него.
Например: «Если треугольник имеет четыре стороны, то 2 + 2 = 4». Такое высказывание в обыденной речи будет встречено с легким недоумением, но вы должны хорошо понимать, что это пример операции импликации. По определению, из ложной посылки «Если треугольник имеет четыре стороны», может следовать какое угодно заключение, и сложное высказывание будет истинным.
Поскольку любое истинное высказывание ничем не отличается от другого истинного высказывания, так как никаких других свойств высказываний математическая логика не рассматривает, то все истинные высказывания между собой эквивалентны. Это в равной мере относится и ко всем ложным высказываниям.
Рассматривая с такой точки зрения любые два истинных высказывания, например «Дважды два четыре» и «Наполеон умер 5 мая 1821 года», равно как и любые два ложных высказывания вроде «Дважды два пять» и «Снег черен», трактуются как эквивалентные друг другу.