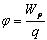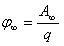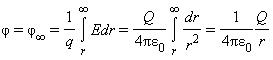Что такое эквипотенциальная поверхность в общем случае

Эквипотенциальные поверхности

Вы будете перенаправлены на Автор24

Графическое изображение полей, можно составить не только с линиями напряженности, но и с помощью разности потенциалов. Если объединить в электрическом поле точки с равными потенциалами, то мы получим поверхности равного потенциала или как еще их называют эквипотенциальные поверхности. В пересечении с плоскостью чертежа эквипотенциальные поверхности дают эквипотенциальные линии. Изображая эквипотенциальные линии, которые соответствуют различным значениям потенциала, мы получаем наглядную картину, которая отражает, как изменяется потенциал конкретного поля. Перемещение вдоль эквипотенциальной поверхности заряда работы не требует, так как все точки поля по такой поверхности имеют равный потенциал и сила, которая действует на заряд, всегда перпендикулярна перемещению.

Следовательно, линии напряженности всегда перпендикулярны поверхностям с равными потенциалами.

Наиболее наглядная картина поля будет представлена, если изображать эквипотенциальные линии с равными изменениями потенциала, например в 10 В, 20В, 30 В и т.д. В таком случае скорость изменения потенциала будет обратно пропорциональна расстоянию между соседними эквипотенциальными линиями. То есть густота эквипотенциальных линий пропорциональна напряженности поля (чем выше напряженность поля, тем теснее изображаются линии). Зная эквипотенциальные линии, можно построить линии напряженности рассматриваемого поля и наоборот.

Следовательно, изображения полей с помощью эквипотенциальных линий и линий напряженности равнозначны.

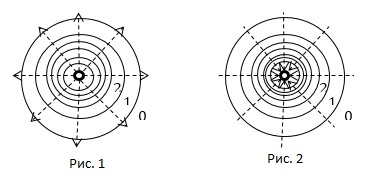
Нумерация эквипотенциальных линий на чертеже

Довольно часто эквипотенциальные линии на чертеже нумеруют. Для того, чтобы указать разность потенциалов на чертеже, произвольную линию обозначают цифрой 0, возле всех остальных линий расставляют цифры 1,2,3 и т.д. Эти цифры указывают разность потенциалов в вольтах избранной эквипотенциальной линии и линии, которую выбрали нулевой. При этом отмечаем, что выбор нулевой линии не важен, так как физический смысл имеет только разность потенциалов для двух поверхностей, и она не зависит от выбора нуля.

Поле точечного заряда с положительным зарядом

Что очевидно из формулы, которая определяет потенциал поля точечного заряда при нормировке потенциала на бесконечность ($\varphi \left(\infty \right)=0$):

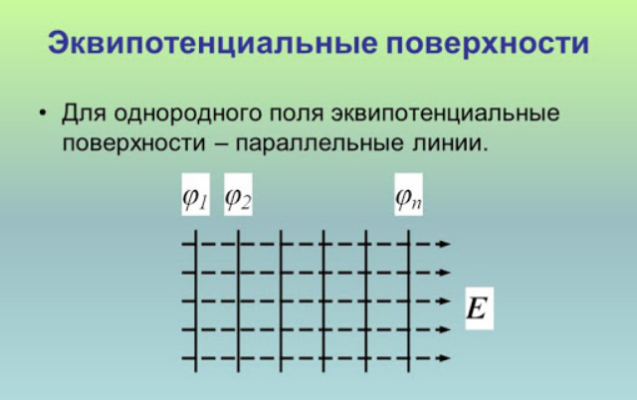
Система параллельных плоскостей, которые находятся на равных расстояниях друг от друга, является эквипотенциальными поверхностями однородного электрического поля.

Готовые работы на аналогичную тему

Задание: Потенциал поля, создаваемый системой зарядов, имеет вид:

Запишем уравнение (1.1) в каноническом виде:

Задание: Потенциал поля, имеет вид:

Перепишем уравнение (1.1) в виде:

Перепишем уравнение (1.1) в виде:

Мы получили каноническое уравнение двуполостного гиперболоида, его полуоси:

Перепишем уравнение (2.5) в виде:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 03 12 2021

Источник

Эквипотенциальные поверхности

Всего получено оценок: 208.

Всего получено оценок: 208.

Одним из способов описания электрического поля являются эквипотенциальные поверхности. Рассмотрим подробнее смысл и метод построения таких поверхностей.

Потенциал электрического поля

Поскольку со стороны электрического поля на заряд действует сила, при перемещении заряда полем совершается некоторая работа (положительная, если заряд перемещается по направлению вектора силы, и отрицательная в противоположном случае). Следовательно, электрическое поле обладает некоторой потенциальной энергией.

Сила, действующая на заряд, пропорциональна этому заряду. А значит, потенциальная энергия поля также будет пропорциональна ему. Коэффициент пропорциональности, равный отношению потенциальной энергии поля к величине заряда, является энергетической характеристикой данного поля, и называется потенциалом:

Отметим, что потенциал пропорционален напряженности электрического поля, и численно равен работе, которая совершается, при удалении единичного заряда из этого поля (перемещения на бесконечное расстояние).

Эквипотенциальная поверхность

Если рассмотреть поле, создаваемое точечным зарядом, то его напряженность падает по мере удаления от заряда в любом направлении. Следовательно, по мере удаления происходит и уменьшение потенциала поля. При этом в пространстве вокруг заряда можно указать ряд точек, обладающих одинаковым потенциалом.

Напомним, что точки, равноудаленные от некоторой заданной, образуют сферу. А значит, точки вокруг точечного заряда, обладающие одним и тем же потенциалом, также будут образовывать сферу с центром, лежащим в точечном заряде. Важное свойство этой сферы – при перемещении заряда по ней работа поля равна нулю, поскольку потенциальная энергия во всех точках этой поверхности одинакова. Нулевая работа перемещения также следует из того факта, что вектор напряженности перпендикулярен этой сфере (а значит, и направлению перемещения).

Поверхность, образованная точками с одним потенциалом, называется эквипотенциальной. Силовые линии и эквипотенциальные поверхности всегда взаимно перпендикулярны, а значит, работа поля по перемещению заряда по эквипотенциальной поверхности равна нулю. Плотность расположения эквипотенциальных поверхностей характеризует скорость изменения потенциала в данной области. Чем гуще расположены эквипотенциальные поверхности, тем быстрее меняется потенциал при движении перпендикулярно им.

Для однородного поля, например, созданного двумя заряженными пластинами, эквипотенциальные поверхности представляют собой плоскости, параллельные пластинам. И в этом случае также перемещение заряда по любой поверхности равного потенциала происходит перпендикулярно вектору напряженности, а значит работа поля по перемещению равна нулю.

Рис. 2. Эквипотенциальные поверхности однородного поля.

Для поля, образованного несколькими зарядами, эквипотенциальные поверхности имеют более сложную конфигурацию, однако, и в этом случае линии напряженности перпендикулярны этим поверхностям. Например, эквипотенциальные поверхности диполя выглядят следующим образом:

Рис. 3. Эквипотенциальные поверхности диполя.

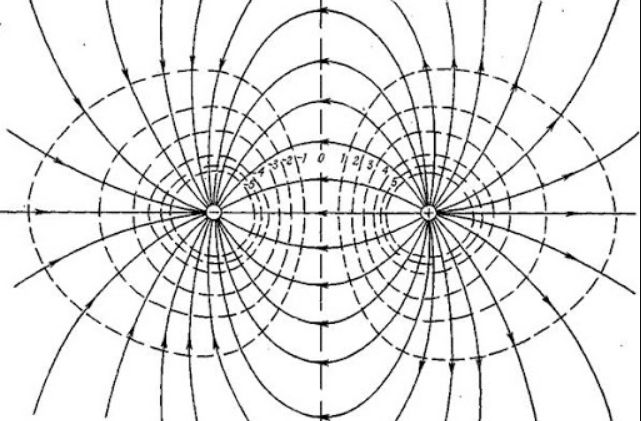
Отметим еще одно интересное свойство эквипотенциальных поверхностей – они могут располагаться плотнее и реже, но никогда не пересекаются.

Что мы узнали?

Потенциал электрического поля пропорционален его напряженности, и численно равен работе, которая совершается, при удалении единичного заряда из этого поля. Точки, в которых потенциал одинаков, образуют поверхность, называемую эквипотенциальной. При перемещении заряда вдоль этой поверхности работа поля равна нулю.

Источник

Эквипотенциальные поверхности. Потенциал электростатического поля

Работа по перемещению заряда из точки А в точку В зависит только от положения точек А и В и не зависит от формы пути, по которому движется пробный заряд. Исходя из этого работа, по перемещению заряда, будет равна убыли потенциальной энергии W данного заряда:

Если работа зависит только от положения начала и конца пути в электростатическом поле, то она может быть выражена как разница двух чисел.

Возьмем производную точку М и обозначим работу по перемещению пробного заряда q_пр от М к А через φ(А), а от М к В через φ(В). После чего будет осуществлено перемещение данного заряда от А к В по пути А- М – В.

Так как работу перехода М – А мы обозначили как φ(А), то обратный переход А – М также будет φ(А), из чего следует формула:

Положение точки М по сути безразлично, так как в данном случае играет роль только разность значений функций φ. Однако, задав координаты точки М мы однозначно определим величины функций φ(А) и φ(В), хотя на величину разности φ(А) — φ(В) положение точки М никак не влияет. Как только координаты точки М выбраны, число φ определяется в любой точке пространства.

Отсюда следует важный вывод – величина φ является функцией координат x, y, z и скаляром электростатического поля. Данная скалярная функция φ называется потенциалом электростатического поля. Точка отсчета М для удобства расчетов помещается в бесконечность. Потенциал бесконечно удаленной точки принимают равным нулю φ = 0.

Физическая величина, которая равна отношению потенциальной энергии, приобретаемой положительным зарядом q_пр, при его переносе из бесконечности в данную точку пространства к этому заряду, то есть:

Потенциал – это энергетическая характеристика поля. Численно он равен работе, которую нужно совершить при перенесении единичного заряда из бесконечности, где потенциальная энергия считается равной нулю, в данную точку поля.

Из формул (2) и (формулы 3 приведенной по следующей ссылке) получим выражения потенциала поля, которое создано точечным зарядом:

Когда поле образуется несколькими расположенными произвольно зарядами q₁, q₂,… q_n, его потенциал φ в данной точке будет равен алгебраической сумме потенциалов φ₁, φ₂, … φ_n, которые создает каждый заряд в отдельности:

Если заряды q₁, q₂,… q_n можно считать точечными, то суммарный потенциал можно посчитать по формуле:

Где r₁, r₂, … r_n расстояние от зарядов q₁, q₂, … q_n до данной точки поля.

В случае если поле образовано электрическим диполем, то потенциал в какой-либо точке поля, находящейся от центра диполя на расстоянии r можно определить по формуле:

Где р = q·l – электрический момент диполя (где l – это плечо диполя), а α – угол между плечом диполя l и радиус вектором r.

В случае, когда точка лежит на оси диполя α = 0, потенциал в этой точке будет равен:

Где φ₁ и φ₂ потенциалы в точках А и В или

Отсюда следует, что совершаемая полем работа по перемещению заряда измеряется произведением заряда q / , переносимого в электростатическом поле, на разность потенциалов конечной (φ₂) и начальной (φ₁) точек пути и никак не зависит от формы пути.

Совокупность точек с одинаковым потенциалом образуют эквипотенциальную поверхность или поверхность равного потенциала (φ = const). С помощью данных точек эквипотенциальную поверхность можно изобразить графически.

На рисунке ниже изображено электрическое поле равномерно заряженного диска, где пунктирные линии – эквипотенциальные поверхности, а сплошные – линии напряженности.

Данный рисунок иллюстрирует общее свойство эквипотенциальных поверхностей и силовых линий – эквипотенциальная поверхность и силовая линия, проведенная через любую точку, в данной точке взаимно перпендикулярны. Поскольку все точки эквипотенциальной поверхности имеют одинаковый потенциал (φ₁ – φ₂ = 0), то работа не совершается при перемещении заряда вдоль нее. Из этого следует, что действующий на заряд вектор силы, а значит и вектор напряженности все время перпендикулярен к перемещению.

Если заряд перемещается по эквипотенциальной поверхности (φ = const), то работа поля будет равна нулю:

В общем случае совершаемая полем работа по перемещению заряда q / будет равна:

Где dS – элементарное перемещение, а Е – проекция вектора напряженности Е на направление перемещения.

В результате интегрирования выражения (11) для однородного поля получим:

Где S – путь, а α – угол между направлением вектора Е и перемещения.

Источник

Как сказал.

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Я учу детей тому, как надо учиться

Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.

Урок 25-2. (дополнительный материал) Эквипотенциальные поверхности

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Во многих задачах электростатики при вычислении потенциалов за начальную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал φ_∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности.

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.

Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рисунке представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.

Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей

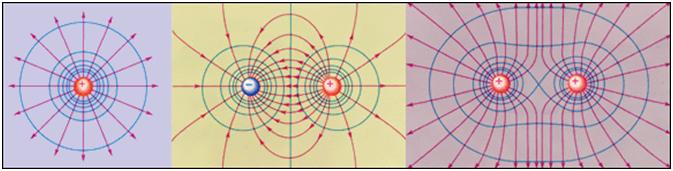
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.

Свойства эквипотенциальных поверхностей:

Источник

Эквипотенциальные поверхности

Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.

Эквипотенциальная поверхность в любой точке должна быть перпендикулярна направлению напряженности электрического поля. Если бы это было не так (т. е. если бы существовала компонента Е, параллельная поверхности), то для перемещения заряда вдоль поверхности в направлении, противоположном этой компоненте Е, приходилось бы совершать работу, что противоречит предположению об эквипотенциальности поверхности.

Тот факт, что силовые линии электрического поля перпендикулярны эквипотенциальным поверхностям, помогает построению эквипотенциальных поверхностей, если известно расположение силовых линий.

На рис. 24.2 изображено несколько эквипотенциальных линий (штриховые линии) для поля между параллельными пластинами, разность потенциалов которых составляет 20 В. Эти линии принадлежат эквипотенциальным поверхностям, которые пересекают рисунок перпендикулярно плоскости книжной страницы. Потенциал отрицательной пластины условно принят за нулевой; указан соответствующий потенциал каждой эквипотенциальной линии. Эквипотенциальные линии для случая двух равных по величине и противоположных по знаку зарядов показаны штриховыми линиями на рис. 24.3.

В одном из разделов ранее мы видели, что в статическом случае внутри проводника не существует электрическое поле, так как в противном случае на свободные электроны действовала бы сила и они пришли бы в движение. Иными словами, в статическом случае проводник должен находиться целиком под одним и тем же потенциалом, и поверхность проводника является, таким образом, эквипотенциальной. (Иначе свободные электроны на поверхности пришли бы в движение.) Это полностью согласуется с уже отмеченным выше фактом, что электрическое поле у поверхности проводника перпендикулярно поверхности.

Продолжение следует. Коротко о следующей публикации:

Электрон-вольт, единица энергии.
Один электрон-вольт равен энергии, которую приобретает электрон, проходя разность потенциалов 1 В.

Замечания и предложения принимаются и приветствуются!

Источник