Что такое численность конечного множества
Число элементов объединения и разности двух конечных множеств
Урок 1,2 ТЕОРИЯ МНОЖЕСТВ
Множество – это совокупность объектов (в математике или окружающей действительности), сгруппированных по какому-либо признаку.
Обозначают множество заглавной латинской буквой, например, множество А, множество В.
Множество – не значит «много». Множество может состоять из большого числа элементов, из нескольких элементов или из одного элемента. А так же множество может вообще не содержать ни одного элемента. Такое множество называют «пустое множество» и обозначают символом Ø
Элементы множества – это объекты или предметы, составляющие множество. Обозначают строчными латинскими буквами: a, b, c, d, t, f и т.д.
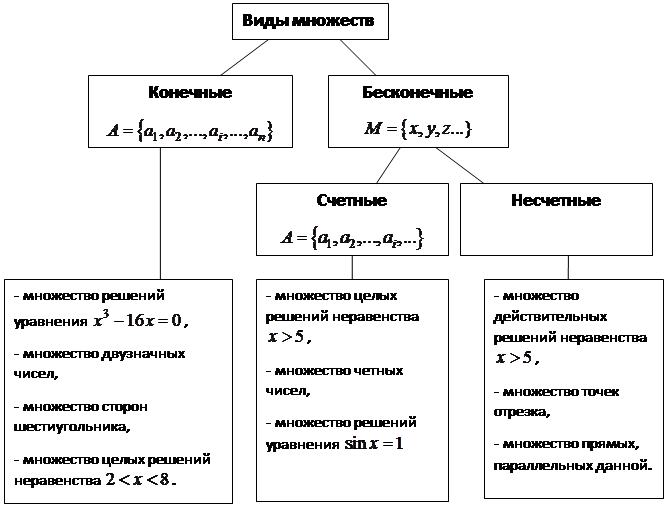
Множества бывают конечные и бесконечные. Например, множество всех двухзначных чисел – конечное. Множество всех целых чисел – бесконечное. Для некоторых числовых множеств в математике приняты стандартные обозначения:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
R – множество действительных чисел.
Способы задания множеств
1. Пересечением (применяется только для конечных множеств). Все элементы множества записывают в фигурных скобках.
Например, множество всех чётных однозначных чисел запишем так:
2. Характеристическими свойствами (когда элементов очень много или множество является бесконечным).
Например, множество В =
Зададим то же самое множество с помощью характеристических свойств:
а) б) в) г) д)
 |
Число элементов объединения и разности двух конечных множеств
Пусть A и B — конечные множества. Число элементов множества A условимся обозначать символом m(A) и называть численностью множества A.
Определим численность объединения множеств A и B.
Если множества A и B не пересекаются (см. рис. 1а), то m(AÈB) = m(A) + m(B). Таким образом, численность объединения конечных непересекающихся множеств равна сумме численностей этих множеств.
Определим теперь численность разности множеств A и B.
Если множества A и B не пересекаются (см. рис. 1а), то A \ B = A, и поэтому m(A\B) = m(A).
Примеры решения задач
Задача 1. Каждый студент первого курса обязан изучать хотя бы один иностранный язык. На юридическом факультете изучаются либо английский, либо немецкий язык. Из 94 первокурсников юридического факультета 76 человек изучают английский язык, 34 – изучают немецкий. Сколько студентов изучают два языка?
Решение. Обозначим А – множество студентов, изучающих английский язык; В – множество студентов, изучающих немецкий язык. Множество всех первокурсников равно АÈВ. Множество, изучающих два языка AÇB. Воспользуемся формулой
Из условия задачи m(A)=76, m(B)=34, m(AÈB) =94. Поэтому
Дата добавления: 2020-11-23 ; просмотров: 312 ; Мы поможем в написании вашей работы!
Конечное множество
Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным.
Содержание
Формальное определение
Два множества 
и 
называются эквивалентными, если существует биективное отображение одного множества в другое. Если множества X и Y эквивалентны, то этот факт записывают 
или 
и говорят, что множества имеют одинаковые мощности.
Множество 
называется конечным, если оно эквивалентно множеству 
при некотором неотрицательном целом 
. При этом число называется количеством элементов множества , что записывается как 
. [1]
В частности, пустое множество является конечным множеством, количество элементов которого равно 0, то есть, 
.
Свойства
См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Конечное множество» в других словарях:
конечное множество — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN finite set … Справочник технического переводчика
МНОЖЕСТВО — МНОЖЕСТВО, множества, ср. (книжн.). 1. только ед. Неопределенно большое количество, число чего нибудь. Множество рабочих. Множество фактов. «Я слышал в жизни множество отличнейших певцов.» Некрасов. 2. Совокупность элементов, выделенных в… … Толковый словарь Ушакова
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия
Конечное — то, что имеет предел, границу, конец. В философии понятие К. используется как категория, характеризующая всякий определённый, ограниченный объект (вещь, процесс, явление, состояние, свойство и т. д.). Каждый познаваемый объект… … Большая советская энциклопедия
Разрешимое множество — В теории множеств, теории алгоритмов и математической логике, множество натуральных чисел называется разрешимым или рекурсивным, если существует алгоритм, который, получив на вход любое натуральное число, через конечное число шагов завершается и… … Википедия
Дескриптивное множество — Дескриптивное множество конечное множество, каждому элементу которого поставлено в соответствие неотрицательное число («вес»)[1]. В случае фиксированного для определённого исследования элементов дескриптивного множества, можно использовать… … Википедия
Перечислимое множество — Не следует путать с счётным множеством. В теории множеств, теории алгоритмов и математической логике, перечислимое множество (эффективно перечислимое, рекурсивно перечислимое, полуразрешимое множество[1]) множество конструктивных объектов… … Википедия
Арифметическое множество — В теории множеств и математической логике, множество натуральных чисел называется арифметическим, если оно может быть определено формулой в языке арифметики первого порядка, то есть если существует такая формула с одной свободной переменной что… … Википедия
Классификация множеств
Основной характеристикой множеств является количество элементов, содержащихся в этом множестве.
По данному признаку выделяются:
1. Множество, содержащее конечное число элементов называется конечным.
Количество элементов конечного множества называют его мощностью.
2. Множество, не являющееся конечным, называется бесконечным.
3. Если множество не содержит элементов, то оно называется пустым и обозначается 
.
1. Конечное множество по признаку мощностихарактеризуется:
Два множества А и В называются эквивалентными, или, равномощными, если между их элементами можно установить взаимно-однозначное соответствие.
Пример: Рассмотрим множества, состоящие из букв слов:
; 
; 
; 
.
Множества А, В и С имеют равные мощности: 
, а мощность множества D меньше 
.
При этом, множества А и В равны, а множества А и С – эквивалентны.
Эталоном для сравнения множеств служит натуральный ряд чисел. Поэтому все числовые последовательности, содержащие различные элементы, эквивалентны натуральному ряду чисел, что видно по их индексам.
2. Бесконечное множество, которое эквивалентно множеству натуральных чисел, называется счетным.
Говорим, что все элементы счетного множества пронумерованы.
В противном случае бесконечное множество будет несчетным.
В 1878 году Георг Кантор доказал, что множество точек, расположенных на отрезке от 0 до 1 несчетно.
Во множестве могут быть выделены подмножества.
Если каждый элемент множества K принадлежит множеству М, то множество К называют подмножеством множества М и обозначают 
.
1) множество всех книг данного автора в библиотеке, есть подмножество всех книг в библиотеке.
2) множество студентов, обучающихся на «4» и «5» в группе есть подмножество всех студентов группы.
3) 
четных чисел меньших или равных 6, есть подмножество множества 
.
Пустое множество является подмножеством любого множества.
Количество подмножеств для исходного множества может быть рассчитано.
Для этого познакомимся с термином булеан.
Булеаноммножества М (N(M)) называется множество всех его подмножеств.
Рассмотрим множество 
. Составим все подмножества множества М.
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
.
Подмножества и 
являются несобственными подмножествами множества М,
остальные – 2-15 – это собственные подмножества.
Всего мы нашли 16 различных подмножеств множества М. Это число 16 может выразить: 
.
В общем случае, для любого конечного множества, состоящего из n элементов, число возможных подмножеств равно 
.
Множество U, состоящее из всех возможных элементов, обладающих данным признаком, называется универсальным.
Вопрос 2. Операции над множествами
И свойства операций
Множества изображаются при помощи диаграмм Эйлера-Венна (круги на плоскости).
Элементы множества изображаются точками:
— внутри круга, если они принадлежат данному множеству;
— вне круга, если не принадлежат.
, 
.
Основными операциями над множествами являются операции:
— пересечение,
— объединение,
— разность,
1. Пересечением множеств А и Вназывается множество 
, состоящее из элементов, которые принадлежат одновременно как множеству А так и множеству В.
Пример: Если 
, 
, то 
.
При помощи диаграмм Эйлера-Венна пересечение множеств изображается следующим образом:
2. Объединением множеств А и Вназывается множество 
, состоящее из элементов, которые принадлежат или множеству А или множеству В.
Пример: Если 
, 
, то 
.
При помощи диаграмм Эйлера-Венна объединениемножеств изображается следующим образом:
3. Разностью множеств А и В называется множество 
, состоящее из элементов множества А, которые не принадлежат множеству В.
Пример: Если 
, 
, то 
.
Разность множеств изображается следующим образом:
По диаграмме видно, что 
можно заменить на 
.
4. Симметрической разностью А и Вназывается множество 
, состоящее из элементов множеств А или В, но не принадлежащих этим множествам одновременно.
Пример: Если 
, 
, то 
.
При помощи диаграмм Эйлера-Венна симметрическая разность множеств изображается следующим образом:
5. Дополнением множества А до множества U называется множество 
, состоящее из элементов множества U, которые не принадлежат множеству А.
При помощи диаграмм Эйлера-Венна дополнение множества изображается следующим образом:
Свойства операций
Операции над множествами обладают рядом свойств, похожих на свойства операций сложения и умножения чисел.
| Объединение (сложение) | Пересечение (умножение) |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 ,  |  ,  |
 ,  |  ,  |
Используя эти операции можно выражать одни множества через другие, при этом сначала выполняется операция дополнения, затем пересечения и только затем операции объединения и разности. Для изменения порядка в выражении используют скобки.
Пример. Доказать справедливость следующего равенства и проверить результат на диаграмме Эйлера-Венна: 
.
Решение. Преобразуем по очереди левую и правую части данного равенства:
1) 
. Заменили разность на пересечение с дополнением.
2) 
.
Использовали переход от разности к пересечению, закон де Моргана, свойство дистрибутивности, свойство 
и 
.
После преобразования видно, что левая и правая части равенств одинаковые, следовательно, равенство доказано.
Проверим равенство на диаграмме Эйлера-Венна.