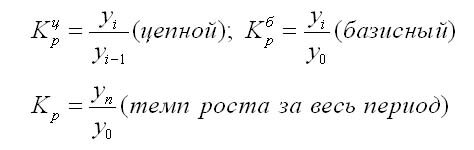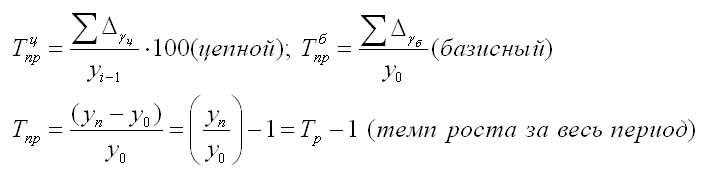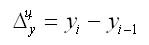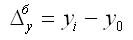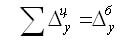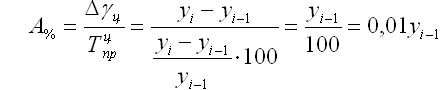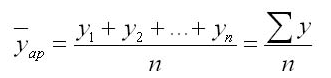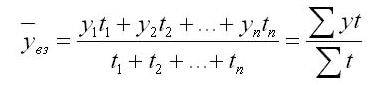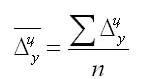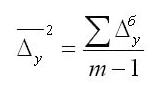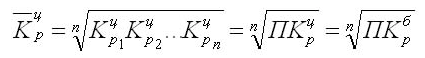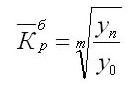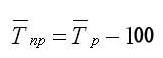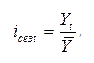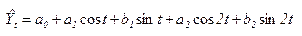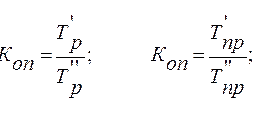Что характеризуют показатели динамики
Ряды динамики
Понимание временных рядов в динамике
Изучение изменений анализируемых показателей во времени, их динамики, является одной из важнейших задач статистики. Эта задача решается путем анализа рядов динамики, также известных как временные ряды.
Ряд динамики, или временной ряд, представляет собой числовые значения определенного статистического показателя, расположенные в хронологическом порядке. Уровни ряда, то есть числовые значения данного статистического показателя, обозначаются буквой y. Начальный уровень ряда y1 называется базисным уровнем, а последний уровень yn — конечным. Моменты или периоды времени, к которым относятся уровни, обозначаются t.
Ряды динамики обычно представляются в виде таблицы или графика. При этом шкала времени t строится по оси абсцисс, а шкала уровней ряда y — по оси ординат.
Пример ряда динамики
| Год | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| На 1 января | 144,2 | 143,5 | 142,8 | 142,2 | 142,0 | 141,9 |
График изменения числа населения России с 2004 по 2009 годы на 1 января
Представленные данные таблицы и графика иллюстрируют постоянное снижение числа жителей России с 2004 по 2009 годы.
Виды рядов динамики
Основные характеристики рядов динамики относятся следующим образом:
При исследовании числа жителей России, ряд динамики обладает следующими основными признаками: 1) моментные значения (доступны данные только на 1 января); 2) выражены в абсолютных величинах (измеряются в миллионах человек); 3) равномерно распределены (интервалы в один год); 4) обособленные события.
Показатели изменения уровней ряда динамики
Анализ динамики рядов начинается с определения, как меняются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Для отслеживания направления и размера изменений уровней во времени рассчитываются показатели изменения уровней рядов динамики:
Все эти показатели могут быть определены в формате базисного способа, когда уровень периода сравнивается с первым (базовым) периодом, или в формате цепного способа — когда сравниваются два уровня соседних периодов.
Базовое абсолютное изменение является разницей между конкретным и первым уровнями ряда, определенная по формуле:
Оно демонстрирует, насколько (в единицах показателей ряда) уровень одного (i-го) периода больше или меньше предшествующего (базисного) уровня и, следовательно, может иметь знак «+» (при удалении уровней) или «–» (при уменьшении уровней).
Цепное абсолютное изменение является разницей между конкретным и предыдущими уровнями ряда, определенная по формуле:
Оно демонстрирует, насколько (в единицах показателей ряда) уровень одного (i-тым) периода больше или меньше предыдущего уровня и может иметь знак «+» или «–».
В следующей расчетной таблице в столбце 3 рассчитаны базовые абсолютные изменения, а в столбце 4 — цепные абсолютные изменения.
| Год | у |  |  |  |  |  , % , % |  ,% ,% |
| 2004 | 144,2 | ||||||
| 2005 | 143,5 | -0,7 | -0,7 | 0,995 | 0,995 | -0,49 | -0,49 |
| 2006 | 142,8 | -1,4 | -0,7 | 0,990 | 0,995 | -0,97 | -0,49 |
| 2007 | 142,2 | -2,0 | -0,6 | 0,986 | 0,996 | -1,39 | -0,42 |
| 2008 | 142,0 | -2,2 | -0,2 | 0,985 | 0,999 | -1,53 | -0,14 |
| 2009 | 141,9 | -2,3 | -0,1 | 0,984 | 0,999 | -1,60 | -0,07 |
| Итого | -2,3 | 0,984 | -1,60 |
Между базисными и цепными абсолютными изменениями существует тесная связь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть

Базисное относительное изменение (базисный темп роста или базисный индекс динамики) определяется как соотношение конкретного и первого уровней ряда, по формуле
Цепное относительное изменение (цепной темп роста или цепной индекс динамики) является соотношением конкретного и предыдущего уровней ряда, по формуле

Относительное изменение показывает, во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (при i>1) или какую его часть составляет (при i Следующая лекция.
Вопрос 3. Показатели динамики. Методы расчета



Индексы изменения – это величины, описывающие изменения уровней динамического ряда. Они включают в себя: абсолютное изменение, коэффициент (темп) изменения, коэффициент (темп) приращения.
В зависимости от базового периода различают базовые и цепные индексы изменения. Базовые индексы изменения – это результат сравнения текущих уровней с одним фиксированным уровнем, принятым за базу. Они описывают окончательные результаты всех изменений в уровнях ряда от базисного периода до текущего. Как правило, начальный уровень динамического ряда принимается в качестве базы. Цепные индексы изменения – это результат сравнения текущих уровней с предшествующими, они описывают интенсивность изменения от периода к периоду.
Методы расчета индексов изменения в зависимости от базового периода приведены в таблице:
| Индексы изменения | Базовые | Цепные |
| Абсолютное изменение Аt | Аt=xt–x0 | аt= xt–xt–1 |
| Коэффициент изменения It | It= xt/x0 | it= xt/xt-1 |
| Темп изменения It×100% | It×100% | it×100% |
| Коэффициент приращения Кt | Кt=(xt–x0)/x0= It–1 | kt=(xt–xt-1)/xt-1=it–1 |
| Темп приращения Кt×100% | Кt×100% | kt×100% |
| <хt> – уровни динамического ряда; х0 – базовый уровень. |
Абсолютное изменение характеризует насколько уровень текущего периода больше или меньше уровня базового или предыдущего периода. Его измеряют в тех же единицах, что и уровни ряда.
Коэффициент изменения показывает во сколько раз уровень текущего периода больше или меньше базового или предыдущего. Этот показатель, выраженный в процентах, называют темпом изменения.
Темп роста показывает, насколько текущий уровень превышает или уступает базовому или предыдущему уровню в процентах.
При анализе цепных показателей динамики получают ряд изменяющихся, частично независимых величин, для которых можно определить средние характеристики обозначенные ниже:
Средний абсолютный рост рассчитывается как среднее арифметическое абсолютных приростов за отдельные периоды времени:
м где n — количество приращений.
Средний коэффициент роста рассчитывается как среднее геометрическое из коэффициентов роста за отдельные периоды времени:
Средний темп роста в течение года определяют с учетом среднего темпа роста:
Показатели динамики: темп роста и темп прироста
Темп прироста
Темп прироста (Tp) — это показатель интенсивности изменения уровня ряда, который выражается в процентах или долях и вычисляется как коэффициент роста (Кп). Кп определяется как отношение текущего уровня к предыдущему или к уровню, используемому в качестве базиса для сравнения. Он показывает, во сколько раз уровень увеличился по сравнению с базовым, или какую часть базового уровня составляет текущий уровень при уменьшении.
Находим коэффициент роста, умножаем на 100 и получаем темп роста
Коэффициент роста можно рассчитать с использованием следующих формул:
Также темп роста можно определить следующим образом:
Темп прироста всегда положителен. Существует определенная взаимосвязь между цепными и базовыми темпами прироста: произведение цепных коэффициентов роста равно базовому коэффициенту роста за весь период, а разница между последующим базовым темпом роста и предыдущим равна цепному темпу роста.
Абсолютный прирост
Рост уровня — это показатель изменения уровня ряда за определенный период времени. Вычисляется по формуле:
1. Цепной рост:
2. Базисный рост:
где уi — уровень периода сравнения;
Уi-1 — уровень предшествующего периода;
У0 — базисный уровень.
Цепной и базисный рост связаны следующим образом: сумма последовательных цепных ростов равна базисному росту за весь временной период:
Рост уровня может быть положительным или отрицательным. Он показывает, насколько уровень текущего периода выше или ниже базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.
Темп прироста
Темп изменения (Ти) показывает относительную величину изменения и позволяет определить, насколько процентов сравниваемое значение отличается от базового значения. Он может быть положительным, отрицательным или равным нулю, а его значение выражается в процентах и долях (коэффициенты изменения); его можно рассчитать как отношение абсолютного изменения к абсолютному базовому значению:
Темп изменения можно выразить через темп роста:
Коэффициент изменения может быть вычислен следующим образом:
Абсолютное значение 1%-го прироста
Перейдем к конкретике. Абсолютное значение 1% изменения (А%) — это соотношение абсолютного изменения к темпу изменения, выраженному в процентах. Это позволяет определить, насколько важно каждое процентное изменение за определенный период времени:
Абсолютное значение одного процентного изменения равно одной сотой части предыдущего или базового уровня. Оно показывает реальное влияние, скрытое за относительным показателем — одним процентным изменением.
Примеры расчетов показателей динамики
Перед тем, как изучать теорию о показателях динамики, вы можете рассмотреть примеры задач по вычислению таких понятий, как темп роста, темп прироста, абсолютный прирост и средние значения динамики.
Понятие показателей динамики
При изучении динамики социальных явлений возникают трудности в описании темпа изменения и расчете средних показателей динамики на основе контрольных данных статистики, которые предлагаются студентам.
Интенсивность изменений во времени анализируется с помощью показателей, которые получаются в результате сравнения уровней. К таким показателям относятся: темп роста, абсолютный прирост и абсолютное значение одного процента прироста. Для обобщенной характеристики динамики исследуемых явлений определяются средние показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут быть определены на основе постоянной или переменной базы сравнения. В данном случае отчетный уровень называется базовым, а уровень с которого производится сравнение — базовым.
Для расчета показателей динамики на постоянной базе, каждый уровень ряда должен быть сравнен с одним и тем же базовым уровнем. В качестве базового уровня используется только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, вычисленные в этом случае, называются базовыми. Для расчета цепных показателей анализа динамики необходимо каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.
Ряды динамики в статистике
Такое стремление изучить зависимость переменных друг от друга наблюдается не только в анализе существующей информации, но и в обнаружении тенденций, которые могут быть связаны друг с другом. Эта задача может быть успешно решена с помощью инструмента «динамические ряды в статистике».
Классическим примером является изменение значений различных показателей в течение определенного промежутка времени. Эти изменения несут в себе информацию не только о попарной зависимости между переменными, но и о динамике изменения самих показателей.
Понятие о рядах динамики
В статистике строгое определение ряда динамики выглядит так.
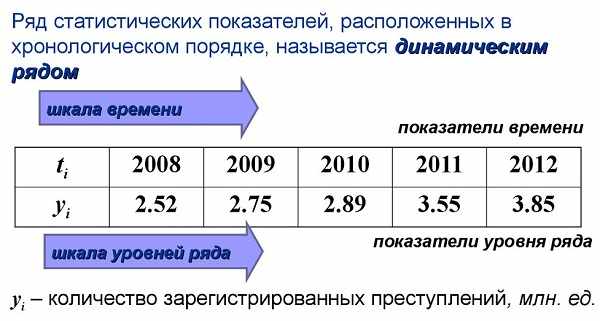
Динамические ряды (иначе говоря, ряды динамики или временные ряды) — это упорядоченные в порядке возрастания дискретные значения выбранного статистического параметра в последовательные временные интервалы.
Если мы рассмотрим временной ряд, станет ясно, что он содержит данные в формате y1t1, y2t2, y3t3…yntn. Для временного ряда показатель y называется «уровнем ряда», при этом первый элемент ряда (у1) является базовым (начальным) уровнем, а уn — конечным уровнем. Показатель t обозначает время, соответствующее каждому уровню ряда.
При построении графика временного ряда функция будет иметь вид t(y), где по оси y (вертикальная ось) отображаются значения уровней ряда (параметр y), а по оси x (горизонтальная ось) — временные значения параметра t.
Пример ряда динамики и его характеристика
Давайте рассмотрим следующий пример ряда информации.
Назвать эту таблицу можно так: «Годовой объем препарата «Ибупрофен» в 2013-2018 гг. в миллионах упаковок»
| Год | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
| Годовой объем, млн. уп. | 88,1 | 91,3 | 96,5 | 99,3 | 101,8 | 100,7 |
В этом ряду можно заметить следующие значения:
Исходя из представленной информации, мы можем заключить, что у нас есть временной ряд.
Виды рядов динамики
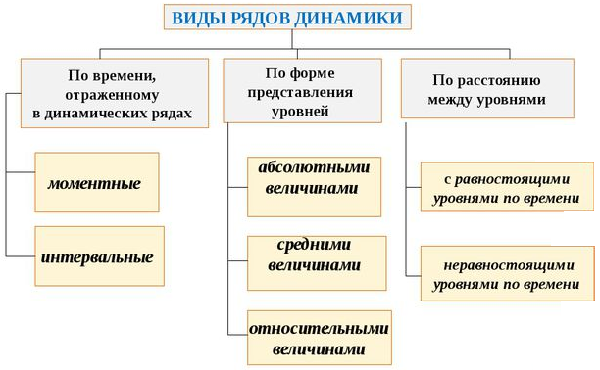
В зависимости от характеристики, динамические ряды подразделяются на несколько типов.
По времени существуют моментальные и интервальные ряды:
По показателю t можно выделить неполные и полные ряды. Неполные ряды характеризуются неравным промежутком между значениями времени, в то время как в полных рядах промежуток равномерен.
Кроме того, существует классификация по числу показателей. Изолированные ряды содержат только один показатель для анализа во времени, а многомерные ряды представляют собой набор параметров, связанных между собой одним процессом.
Правила построения рядов динамики
При построении временных рядов необходимо соблюдать определенные требования:
Характеристики динамики ряда
Главный показатель, определяющий среднее значение абсолютных показателей (y1, y2…yn), является средний уровень ряда. Если основные интервалы не изменяются, то используется формула для его расчета (где t — количество уровней):
Если имеются временные пропуски или они неодинаковы, то методика расчета становится сложнее. Вычисления выполняются с помощью арифметического среднего:
Здесь y1, y2…yn — это абсолютные уровни ряда, a t1, t2…tn — продолжительности временных интервалов.
Для описания используется также средний абсолютный прирост, который представляет собой среднее значение прироста за равные временные интервалы. Если используются гармоничные интервалы, формула будет выглядеть так:
В данном выражении n — количество приростов за выбранный период.
Также существует методика расчета с использованием базисного абсолютного прироста для смыкания рядов с равными интервалами:
Значение m — это количество уровней в выбранном периоде.
Показательный характеристикой является средний темп роста, который отображает изменение уровней ряда (в зависимости от времени). Расчет для цепных показателей производится через вычисление средней геометрической:
В этом выражении n — количество цепных коэффициентов, а Кц — сами цепные коэффициенты.
Если известны все значения уровней, то выражение существенно упрощается:
Иногда требуется характеризовать средний темп прироста, который рассчитывается на основе уже известных средних темпов роста (Тр):
Показатели анализа рядов динамики
В наличии есть 5 характеристик, предназначенные для осуществления анализа:
Анализ сезонных колебаний
Если провести анализ временного ряда, в котором содержатся данные об объемах продаж противовирусных препаратов за последние 5 лет, станет ясно, что ежегодно наблюдается колебание (уменьшение или увеличение) продаж, которые происходят циклично. Это колебание известно как сезонность.
Для того чтобы устранить нежелательное влияние таких колебаний, проводится аналитическое изучение, которое может быть выполнено с применением метода гармонического анализа или учетом сезонных индексов.
Сезонный индекс является фактором, определяющим во сколько раз анализируемый уровень увеличивается или уменьшается относительно среднего уровня:
Здесь Yt – анализируемый уровень, а Ȳ – средний уровень для всего ряда данных.
Более сложный анализ включает выделение гармонических колебаний. Для этого используется разложение на ряд Фурье (гармоники), и выясняется, какие гармоники наиболее соответствуют анализируемому ряду. Общий вид ряда Фурье для двух гармоник представлен следующей формулой:
Индекс сезонности
Для того чтобы избежать необходимости расчета процентного отношения между каждым месяцем во временном ряду, можно вычислить индекс сезонности.
Индекс сезонности рассчитывается с учетом следующих параметров:
Путем сопоставления получается значение, которое в какой-то степени соответствует уровню 100%. При значительном отклонении в меньшую сторону можно говорить о наличии сезонных колебаний.
Приведение рядов динамики к одинаковому основанию
При работе с несколькими явлениями, которые описывают один процесс, возникает интерес к сравнению динамики этих явлений. Чтобы провести корректное сравнение, необходимо привести все ряды к одной базе. Для этого вычисляется коэффициент опережения или отставания.
Каждому ряду присваивается базовый уровень, и также вычисляются темпы роста и прироста для каждого ряда. Для сравнения выбирается аналогичный временной интервал.
Сравнение проводится на основе соотношения базового темпа роста (опционально — прироста) в аналогичном временном интервале. Формулы для расчета достаточно просты:
Аналитическое выравнивание ряда динамики
При анализе временных рядов и прогнозировании трендов часто используется метод аналитического сглаживания. Для этого выбирается математическая функция, которая наиболее точно описывает ряд.
Метод сглаживания интервалов позволяет увеличить временные интервалы, чтобы более точно определить общую тенденцию и понять направление зависимости.
Метод скользящего среднего заключается в усреднении значений временного ряда, чтобы сгладить случайные отклонения от среднего значения. Каждому показателю присваивается уровень, в котором случайные колебания минимизированы.
Метод аналитического сглаживания подбирает зависимость для конкретного ряда, которая наиболее полно отображает алгебраическую связь.
Примеры решения задач на тему «Ряды динамики в статистике»
Упражнением по классике является определение характеристик и показателей для данного показателя динамики.
Задача. Найдите: его тип, цепной и базовый прирост, темп роста/прироста, средний темп прироста для данного временного ряда.
| Отчетный год | Суммарный объем производства, млрд. руб. |
| 2014 | 18 |
| 2015 | 16 |
| 2016 | 17 |
| 2017 | 16 |
| 2018 | 12 |
Согласно определению, данный помеченный показатель динамики относится к интервальному виду, так как он имеет непрерывность во времени. Производим вычисление нужных показателей.
Абсолютные изменения (по цедак основе):
16 – 18 = 2 млрд. руб.
17 – 16 = 1 млрд. руб.
16 – 17 = 1 млрд. руб.
12 – 16 = 4 млрд. руб.
Абсолютные приросты (по базисному подходу):
17 – 18 = 1 млрд. руб.
12 – 18 = 6 млрд. руб.
Темпы роста по цепным показателям:
Темпы роста по базисному подходу:
Темпы прироста по цепным показателям:
Темпы прироста по базисному подходу:
Средний уровень временного ряда:
(18 + 16 + 17 + 16 + 12) / 5 = 15,8.
Среднегодовой абсолютный прирост:
Среднегодовой темп прироста:
А так временные показатели занимают важное положение среди объектов статистики.
Одно из главных преимуществ состояния этих предметов заключается в широкой практической применимости, которая позволяет использовать данную динамику для наблюдений над физическими величинами и экономическими показателями. Очень полезно знать о некоторых деталях, которые поможет правильно проанализировать такую динамику.